Red-Black Tree

1. Introduction of Red Black Tree

Realtime balancing is highest priority on tree as we spoke in previous post.

There were some trials to cope with realtime rebalancing problem.

• AVL Tree, 2-3 Tree, 2-3-4 Tree, B Tree, B+ Tree, B* Tree, Red Black Tree…

Red Black Tree uses Red and Black colors, which corresponds its status as you can assume from the name of the tree.

It was influenced by some of trees, such as 2-3 Tree and B Tree,

Red Black tree is used in Kernel to find out the memory, and scheduling for the processes. It is used for Binder driver or Hash map in Android.

If you deep dive into this tree, it will definately help you to understand kernel or android.

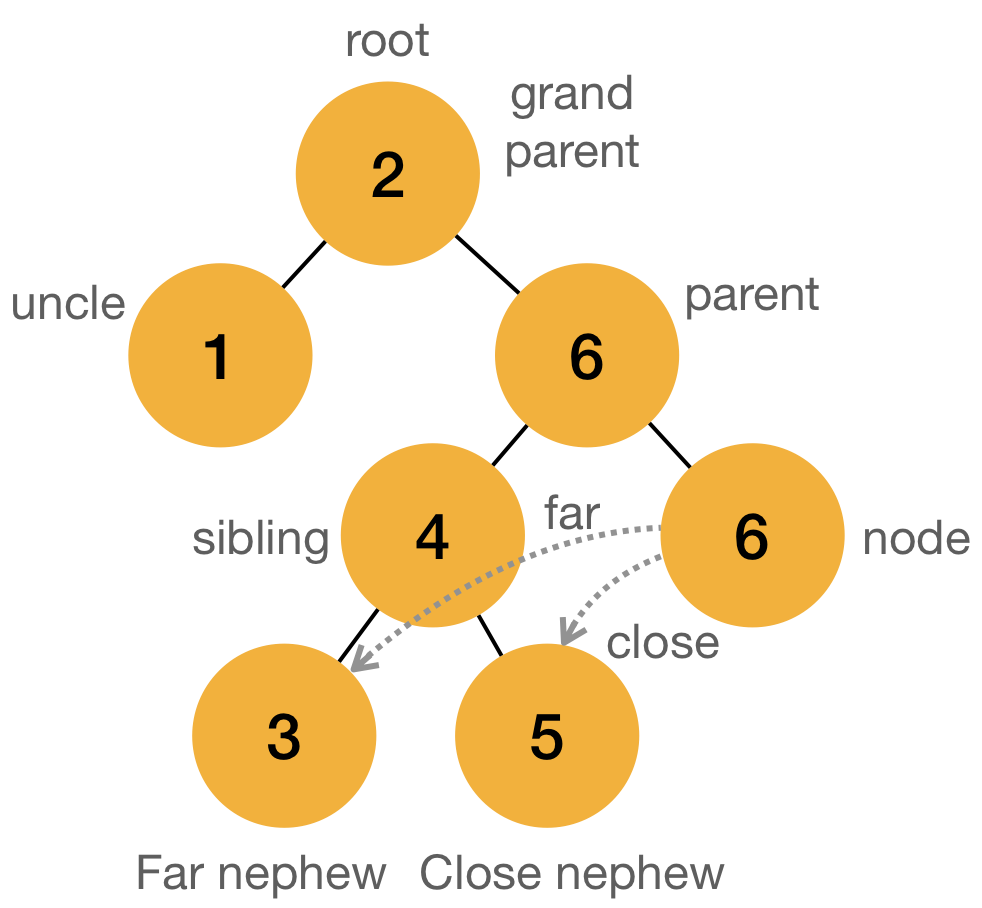
2. Terms

Red Black Tree has two status, Red or Black, and consists of grand parent, parent and node

• Node: Target node
• Parent: Parent node of target node
• GrandParent: Grand parent of target node and parent node of target nodes’ parent node
• Uncle: Another child of grand parent
• Sibling: Another child of parent
• Nephew: Sibling’s children
  • Close nephew: close nephew from the absolute distance perspective, not distance from node to node through each of edges.
  • Far nephew: Far nephew from my position
• Adoption: In complicated tree, some of node which was connected with target nodes need to be linked to other node as a child. That is called adoption

3. Operation

Now, let’s mode deep dive on how it operates. Red-Black Tree has quite complicated rules to support realtime rebalancing. With the following rules, tree can be wel-organized while pushing or popping the data

Before we go, there is Rule#0 for Red-Black Tree. Rule#0 is, if the total number of black node from the root to each of nil node, not leaf node , are same, it is defined well balanced tree in Red-Black Tree concept.

What is nil node?

nil node is not an actual node, but we need to assume that every leaf node should have nil node as it’s children. (and nil node is always black)

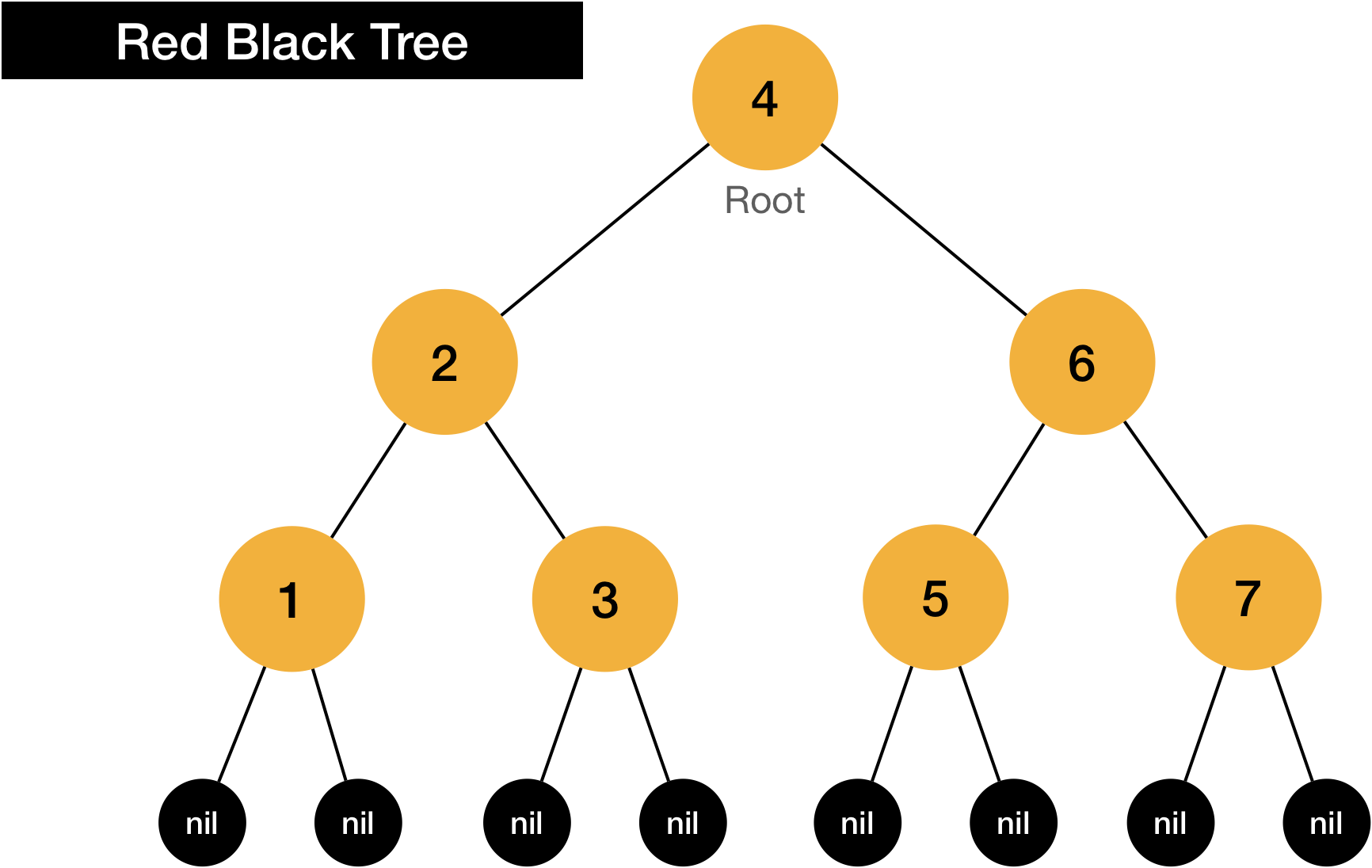
Let’s look at the tree below.

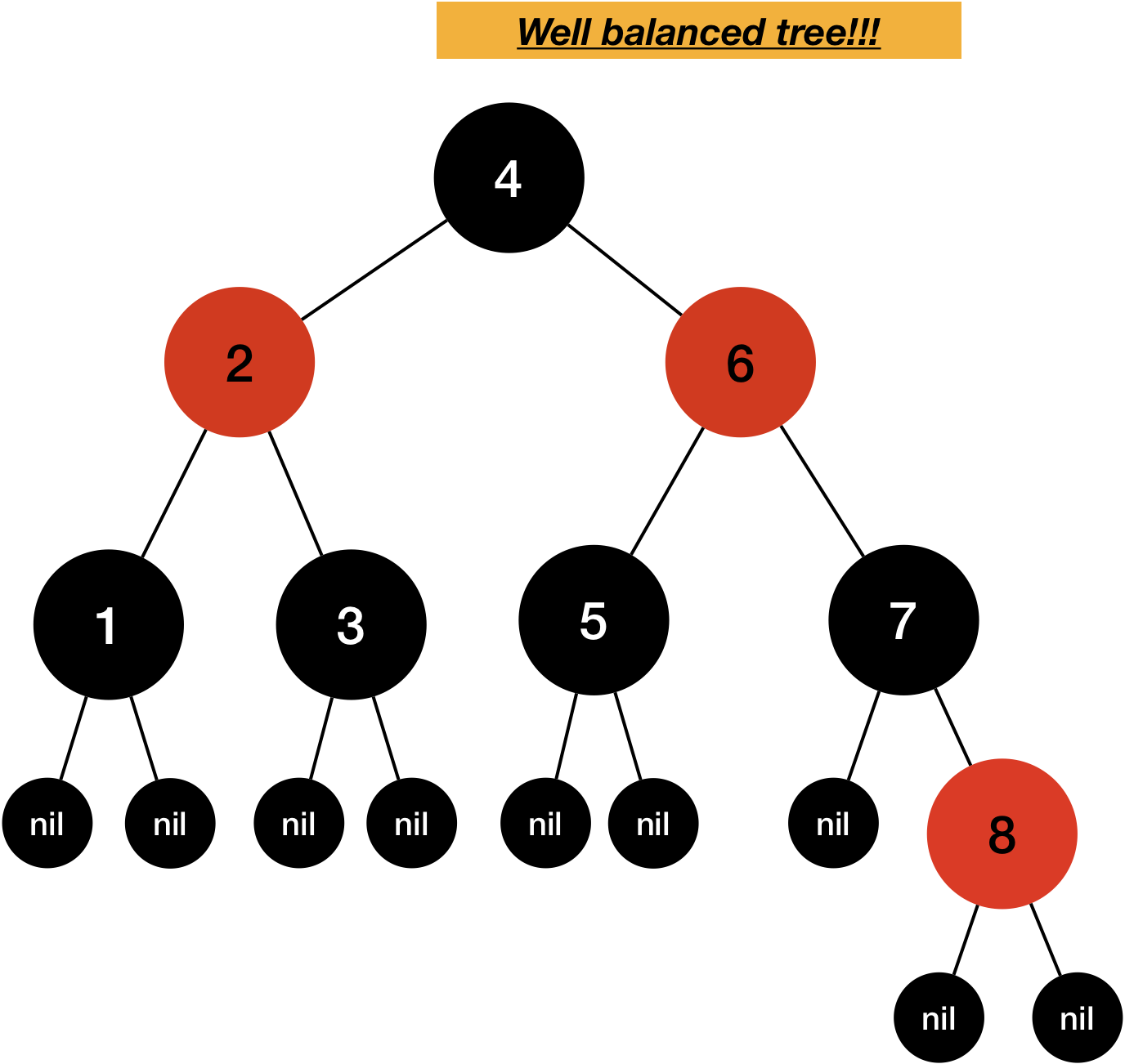
Above is wel-balanced tree and we can see all the route from root to nil node has same number of black nodes.

Look at the figure above. Every path from root to nil has 3 Black nodes including nil node .

Keep in mind and let’s go through how insert works first!

3.1 Insert

3.1.1 Rules

• Common rule: operation described blow should be applied recursively until the nodes are well balanced

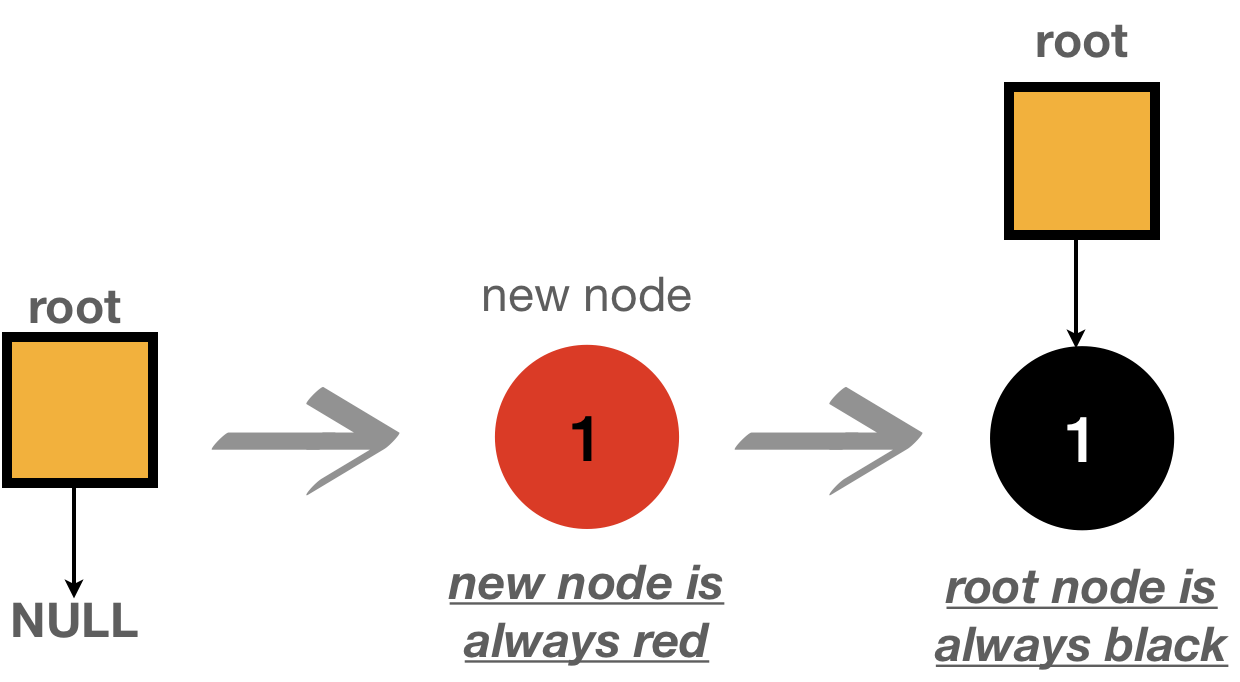
• Rule#1 root node is always Black
• Rule#2 new node is always Red

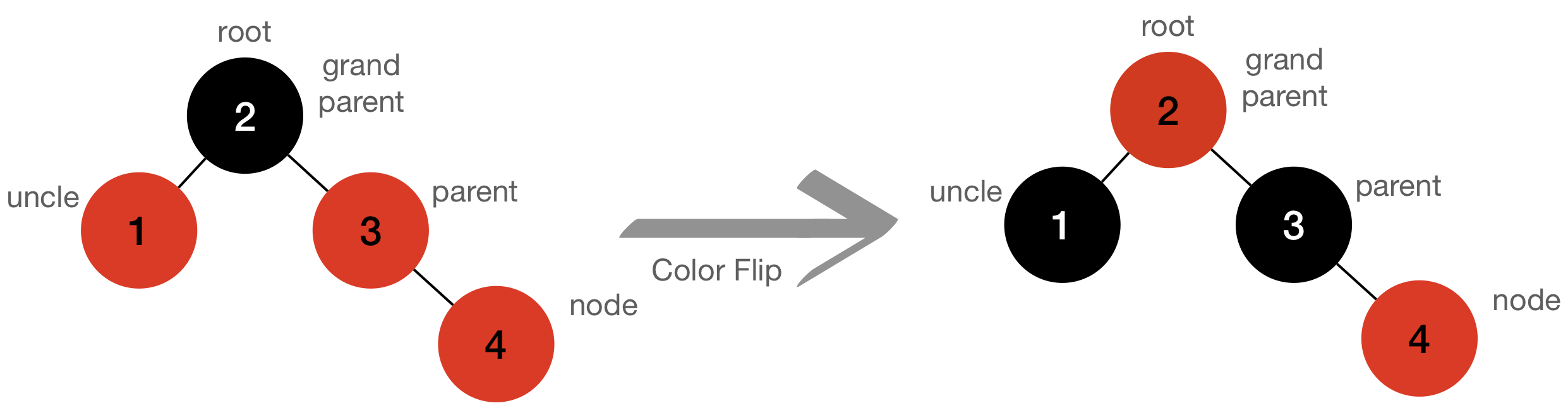
• Rule#3 If parent node is red and uncle node is red as well, flip the colors only
  • parent node’s color will be turned to black
  • grand parent will be switched to red
  • uncle will be changed to black

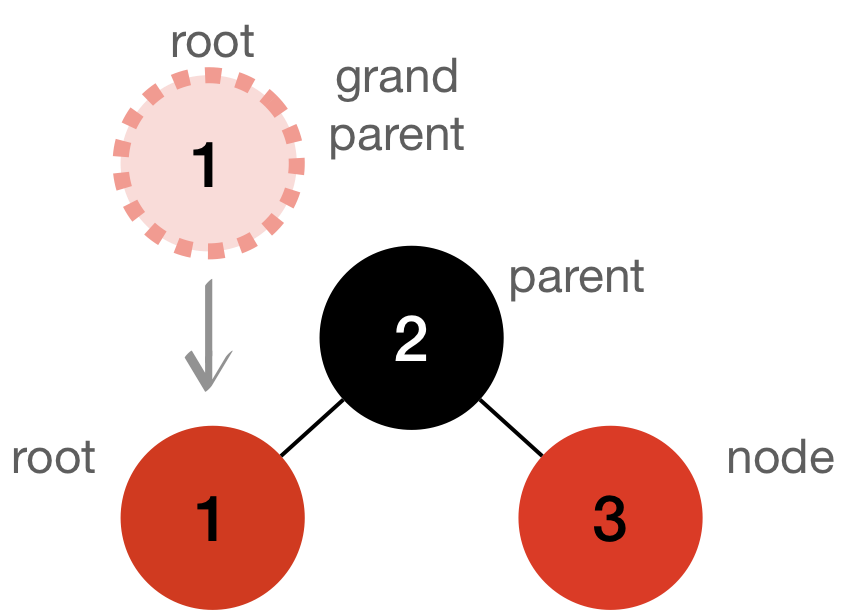
• Rule#4 If parent node is red, rotate the tree and flip the colors
  • Rule#4.1 Flip the colors
    • parent node’s color will be switched to black
    • grand parent ‘s color will be switched to red as it will be always black due to given rules.

- Rule#4.2 Rotate the tree
	- Rotate the tree based on the `where is heavier?` of the tree
		- R-R (Right-heavy)
			- Rotate the tree to the left, which means, grand parent will be the left child of `parent`

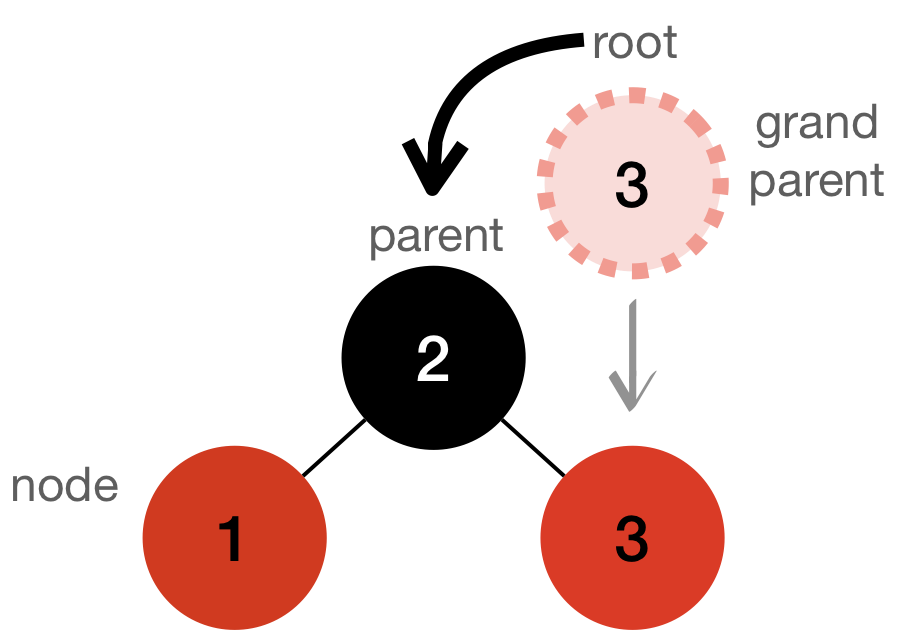
		- L-L (Left-heavy)
			- Rotate the tree to the right

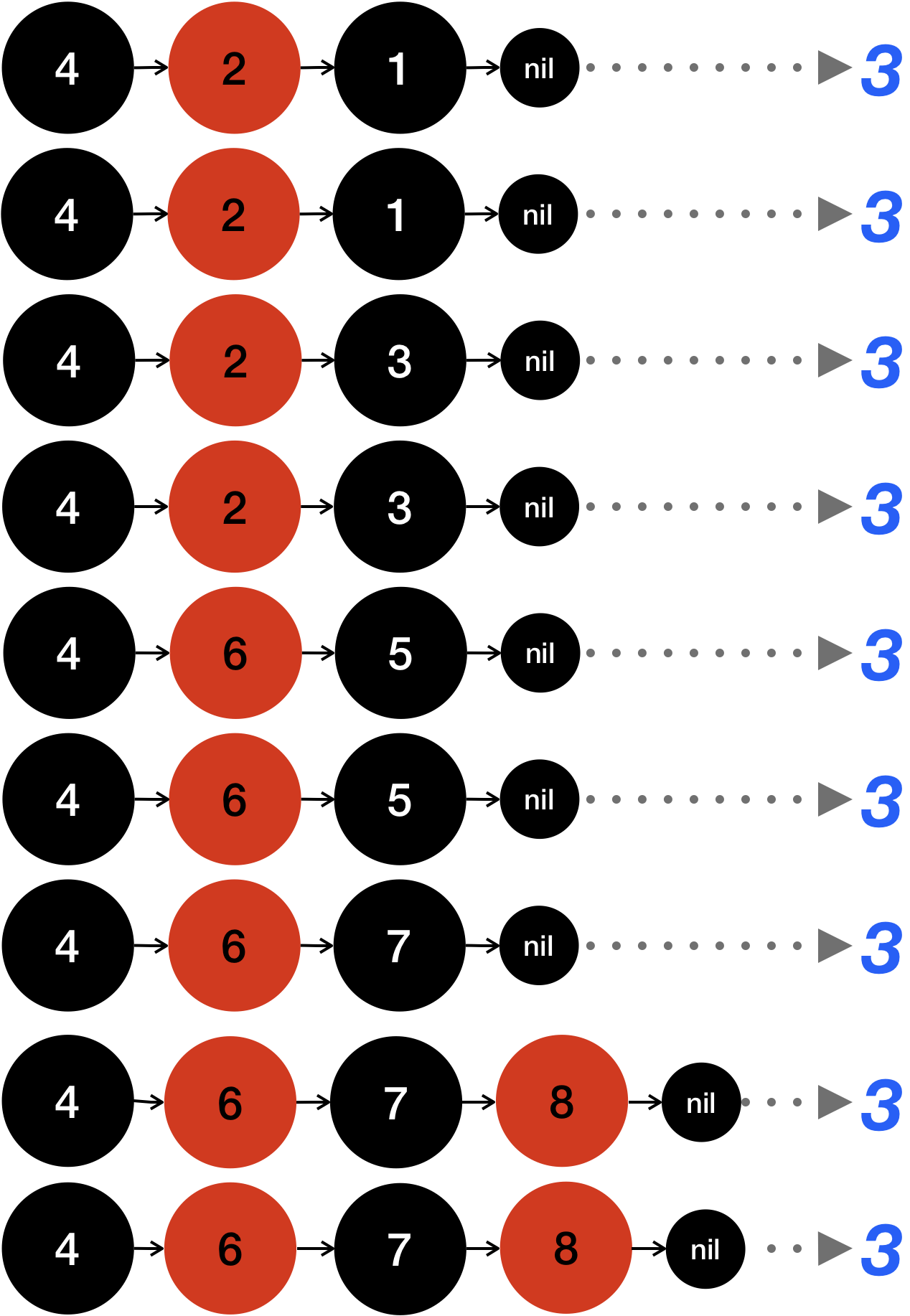
These 4 rules + common rule are all of the insert rule. Now let’s see how the rotation and adoption is happening in complicated tree.

I’ll demonstrate how it works if input is given as input[]={1,2,3,4,5,6,7,8}

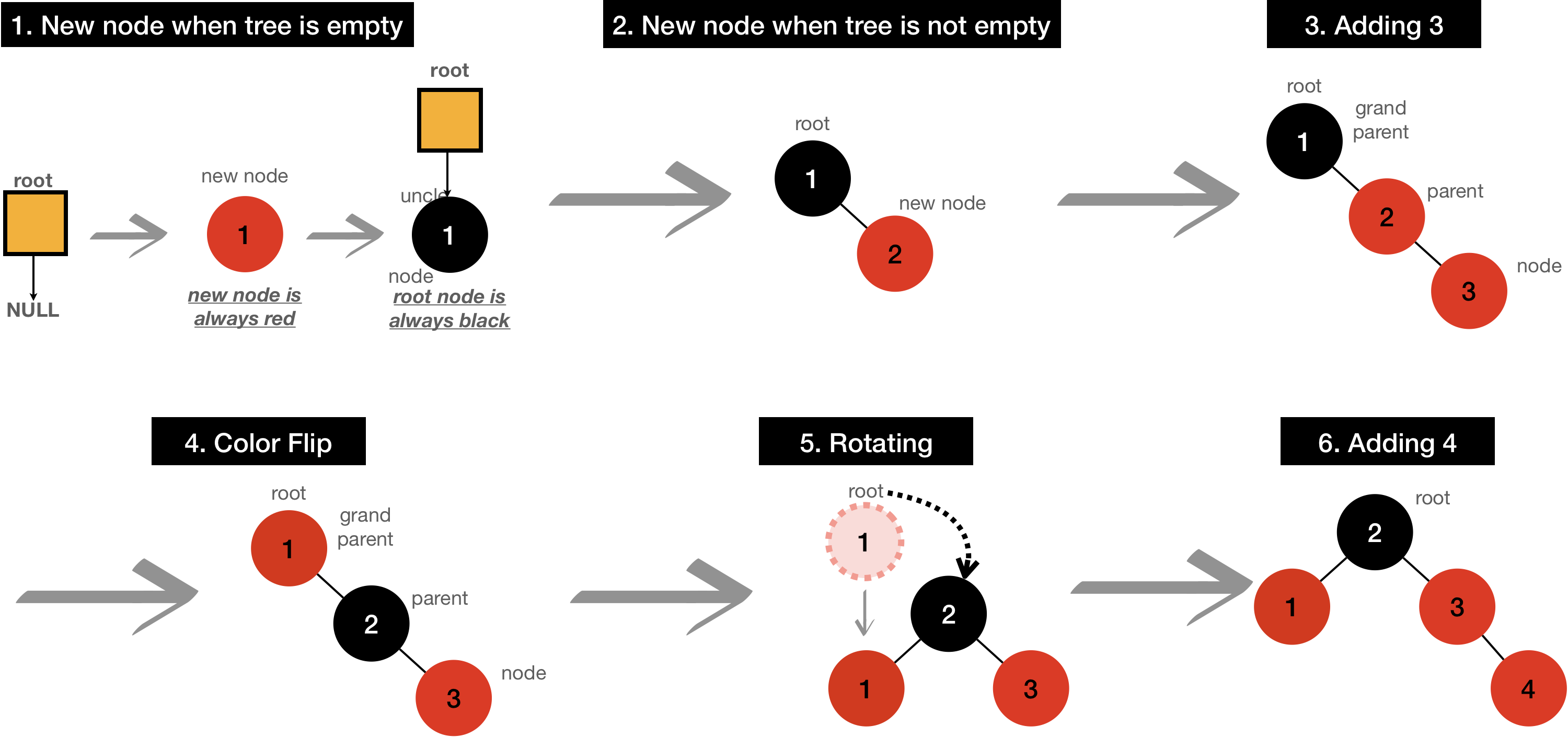
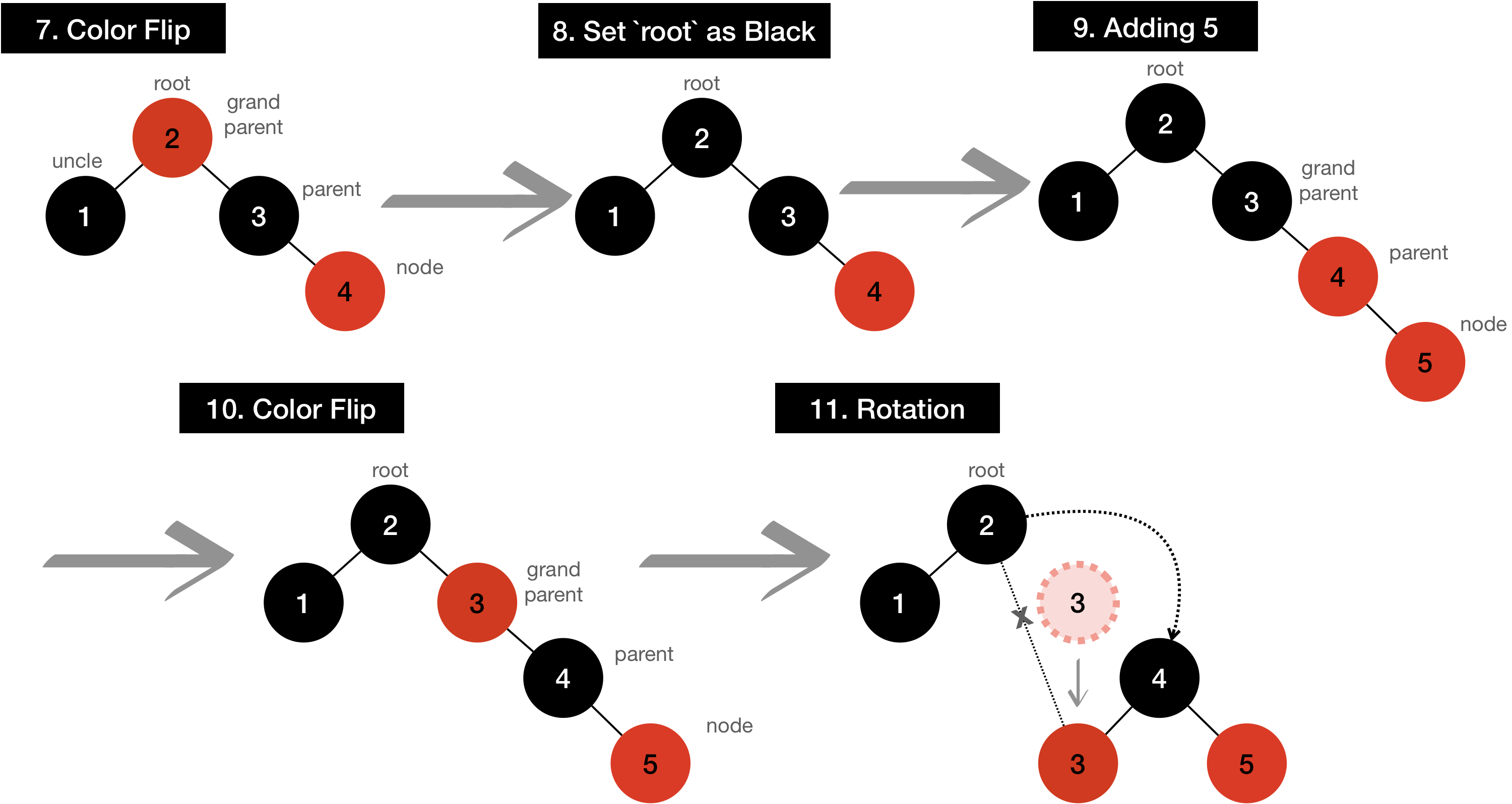
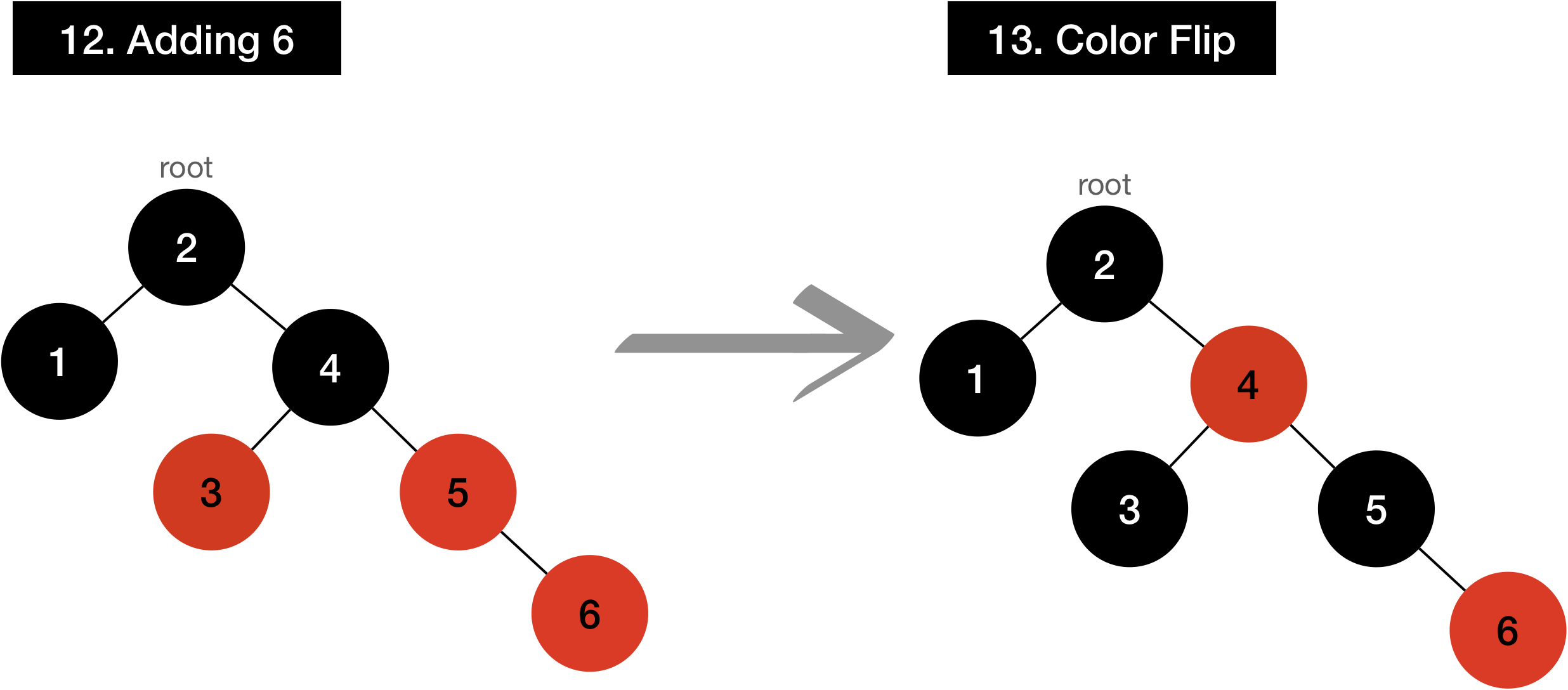
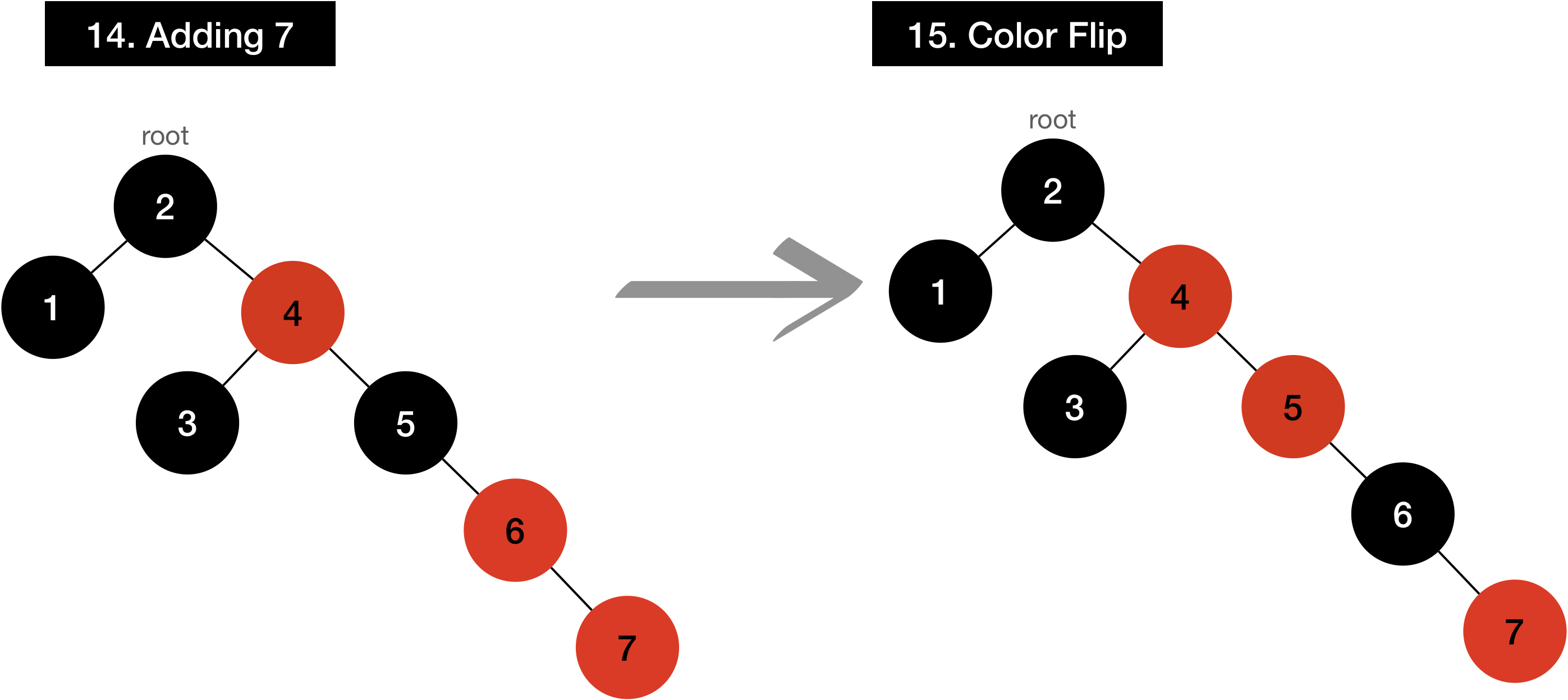
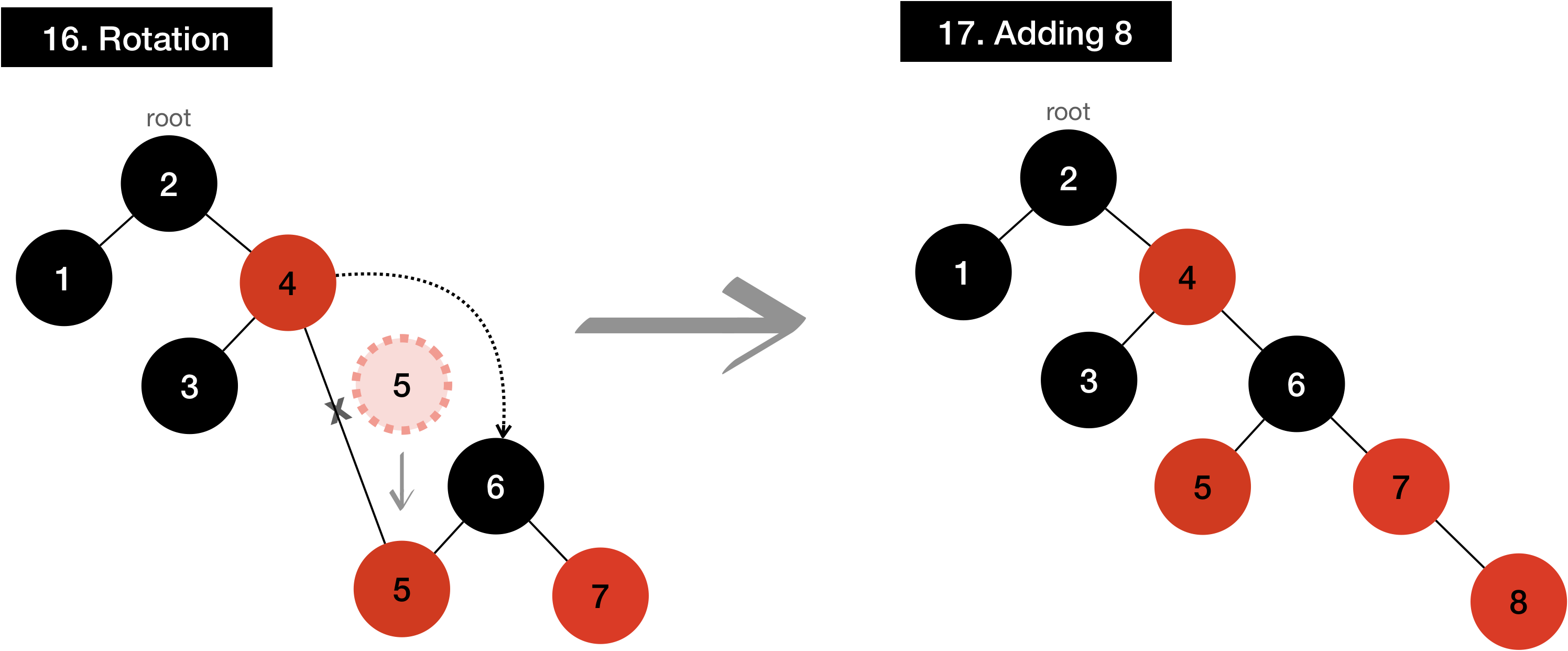
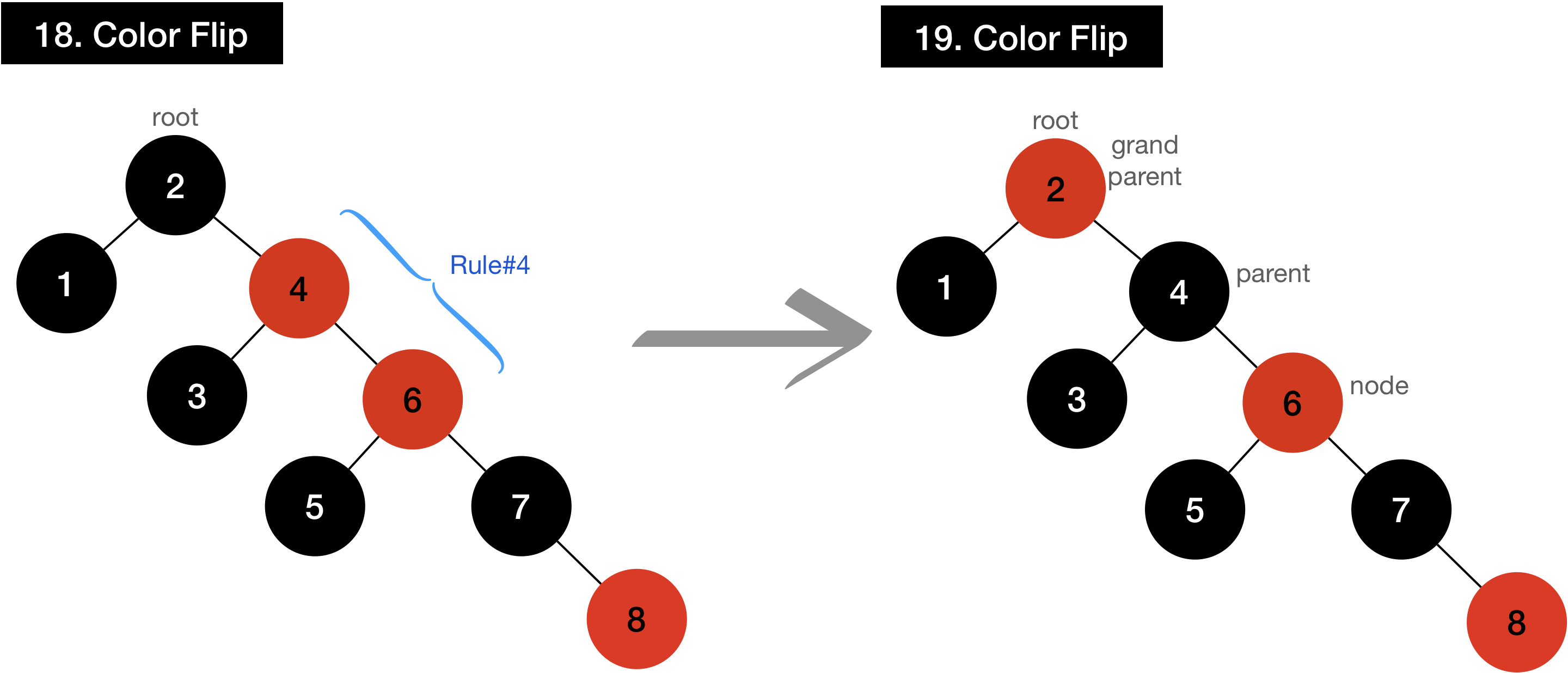
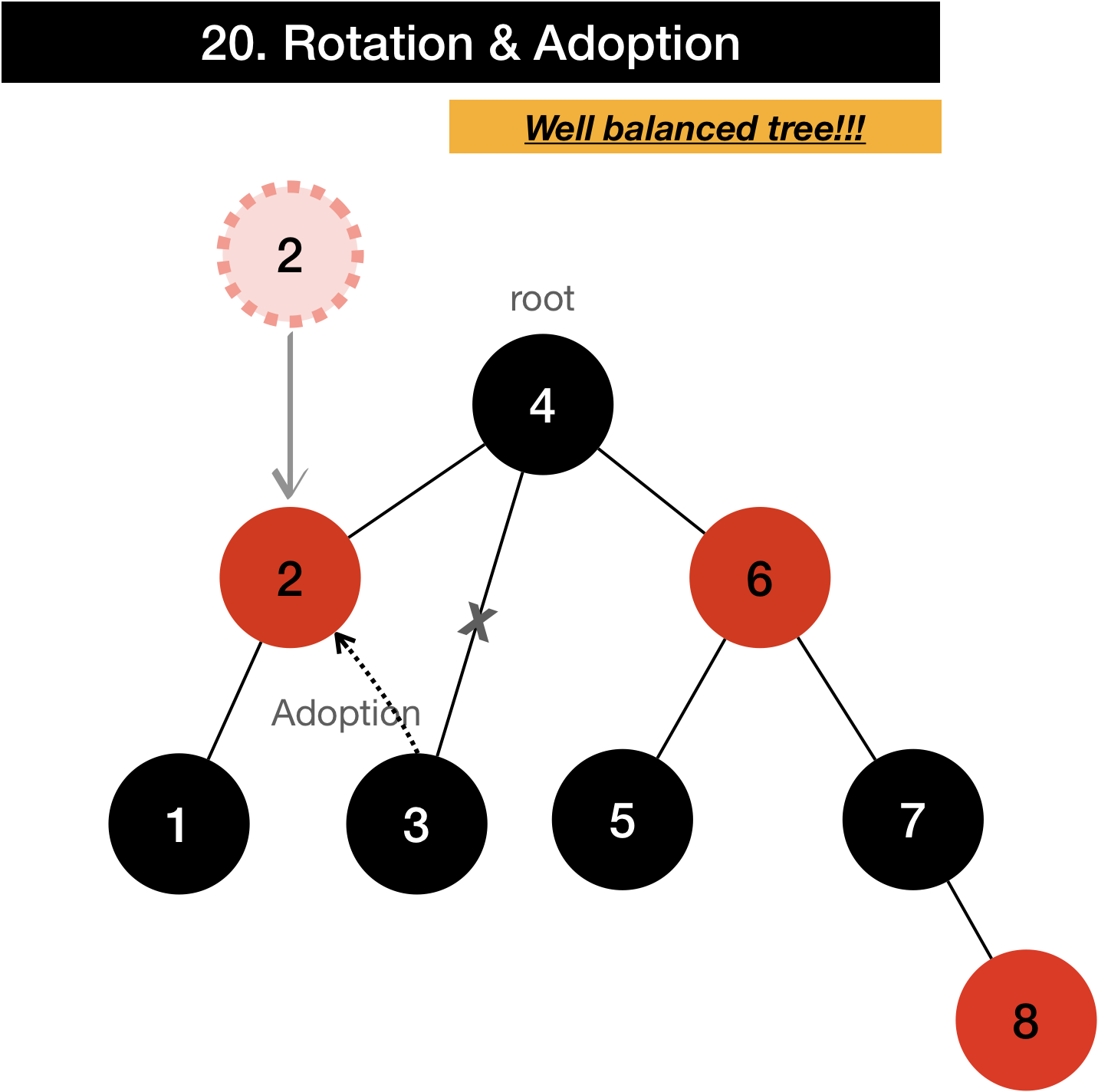
Even though it looks like it’s not balanced until the value 8 is added, it’s well balanced as soon as it’s added.

3.1.2 Implementation

Now let’s talk about implementation part. Even though we have quite straightforward and concrete rule for the tree, it’s quite complicated to write it in code.

Let’s go over the rules step by step again.

First of all, we need to define the node structure, which will have value, color field, left, right and parent pointer. (Parent pointer is useful for reverse traversal from the current node)

enum COLOR{
	RED, BLACK
}
typedef struct _node{
	int data;
	COLOR color;
	struct _node * left;
	struct _node * right;
	struct _node * parent;
} Node;

Node *root = NULL; // root is initiated

and now we can start to implement insert function.

void insert_node(int data){
	Node *newNode = new_node(data);
	Node *parent = NULL;
	Node **current = &root;
	
	while(*current){
		parent = *current; // store current as parent for next step
		if((*current)->data < data) 
			current = &(*current)->right;
		else if((*current)->data > data)
			current = &(*current)->left;
		else
			return;
	}
	newNode->parent = parent;
	*current = newNode;

	if(parent == NULL)
		newNode->color = BLACK; // Rule#1: Root node is always BLACK
	
	__balancing(newNode); // Rebalancing
	
}

Node* new_node(int data){
	Node *node = (Node*)malloc(sizeof(Node));
	node->color = RED; // Rule #2: New Node is always RED
	node->data = data;
	node->left = NULL;
	node->right = NULL;
	node->parent = NULL;
	return newData;
}

First of all, in insert function, we need to focus on how we can find where the new data is placed. Rebalancing is next step.

As we will traverse at the edge of node, pointer will be pointing child of leaf node, a.k.a nil node , we will use double pointer and traverse toward the target in while loop. Once location where the new data should be placed is found, as each of node has parent pointer, its parent and new node will be stored in *current.

I’ll add __ as prefix of balancing function because it is our internal functionality.

void __balancing(Node *node){
	while(node->parent != NULL && // node->parent == NULL means node is root
	node->parent->color == RED && node->color == RED) { // newNode is always RED, and if its parent’s color is also RED, then next action is required

		Node *parent = node->parent;
		Node *gParent = parent->parent;
		Node *uncle = gParent->left; // uncle == left
		if(parent == gParent->left) { // uncle == right
			uncle = gParent->right;
		}

		if(uncle != NULL && uncle->color == RED) { //Uncle exists Uncle is RED —> Rule # 3
			//Color Flip Only
			parent->color = BLACK;
			gParent->color = RED;
			uncle->color = BLACK;
		}
		else { // Uncle is NULL or uncle’s color is BLACK —> Rule#4
			//Color flip
			parent->color = BLACK;
			gParent->color = RED;

			if(parent->right == node){
				//Right-Heavy
				//Rotate to the left
				rotateLeft(node);
			} else {
				//Left-Heavy
				//Rotate to the right
				rotateRight(node);
			}
		}

		root->color = BLACK; // Rule#1 should be written here again as root can always be changed while rotating
		node = gParent; //Change pointer to gParent to see if there is another case that next node(current gParent) and its parent(ggParent) both are RED
	}  
}

In the __balancing function, it should recursively check up if there is condition mismatch cases after rebalancing.

while loop is used to check the status that color of node and its parent both are RED and node is not root. (If node is root, it means that there should be nothing to rebalance)

Set parent, gParent, uncle pointers for the readability of code,

Logics for each of Rules can be quite simply implemented.

• Rule#3: Uncle exists and its color is RED
• Rule#4: Uncle is NULL or its color is BLACK

and as I commented in above code, Rule#1 should be applied in rebalancing code as root can always be changed. and it changes target node to gParent to check if there is any case that is not meeting the rules, especially for the case that Node is RED and its Parent is RED.

For the code readability, I separately wrote the rotating functions. This time, I declared ggParent pointer as re-pointing from ggParent to new child and vice versa are required in the middle of the tree.

void rotateLeft(Node *node){
	Node *parent = node->parent;
	Node *gParent = parent->parent;
	Node *ggParent = gParent->parent;

	if (ggParent) { //ggParent != NULL
		if (ggParent->left == gParent){ //
			ggParent->left = parent;
			parent->parent = ggParent;
		}
		else {
			ggParent->right = parent;
			parent->parent = ggParent;
		}
	}
	else { //ggParent == NULL, which means gParent == root
		root = parent;
		root->parent = NULL;
	}

	if (parent->left){ // if child of current parent exists
		//inherit
		//parent’s child will be always bigger that gParent (target of rotating)
		//that means it will be placed as a right child of new Parent
		gParent->right = parent->left;
		parent->left->parent = gParent;
	}
	else {
		gParent->right = NULL; // clear pointer
	}
	parent->left = gParent; 
	gParent->parent = parent;
}

void rotateRight(Node *node){
	Node *parent = node->parent;
	Node *gParent = parent->parent;
	Node *ggParent = gParent->parent;

	if (ggParent) {
		if (ggParent->left == gParent){ 
			ggParent->left = parent;
			parent->parent = ggParent;
		}
		else {
			ggParent->right = parent;
			parent->parent = ggParent;
		}
	}
	else { 
		root = parent;
		root->parent = NULL;
	}

	if (parent->right){ // if child of current parent exists
		//inherit
		//parent’s child will be always SMALLER that gParent (target of rotating)
		//that means it will be placed as a right child of new Parent
		gParent->left = parent->right;
		parent->right->parent = gParent;
	}
	else {
		gParent->left = NULL; // clear pointer
	}
	parent->right = gParent; 
	gParent->parent = parent;
}

Rotating Left and Right codes are almost same, but only different points are left or right literally.

3.1.3 Test

We will see if implemented code is working properly with multiple inputs. For the first trial of testing, we will set {1,2,3,4,5,6,7,8} as a test vector as we simulated it above.

#include <stdio.h>
#include <stdlib.h>
#include <windows.h>

int main(){

	int vectors[8] = {1,2,3,4,5,6,7,8};
	//int vectors[8] = {8,7,6,5,4,3,2,1};
	for(int i = 0; i < 8; i++){
		system(“cls”);
		insert_node(vectors[i]);
		printf(“[Step #%d]”, i+1);
		display(root);
		getchar();
	}
}

system(“cls”) is a function that we can clear console windows, getchar() is to get char input from the console. Above code will remove printed items from the screen and rewrite tree shape.

Now let’s take a look at display(root) function. Displaying tree in console is quite complicated. Let me introduce most easiest way to display this, in my thought, of course there could be always easier way compare to this.

We have talked about In order traverse before in Binary Search Tree Post. If we use it, we can easily traverse tree, but how we can print it as tree shape?

void display(Node *next){
	if (next == NULL) return;
	static int indent = -1;
	++indent;

	display(next->right);
	for (int i=0;i<indent;i++) printf(“\t”);
	printf(“%d (%c)\n”, next->data, next->color ? ‘B’:’R’);
	display(next->left);

	--indent;
}

We can simply put empty space, I used \t , and indent can be declared as static. Otherwise we can also deliver depth as parameter of recursive function.

//testVector = { 1, 2, 3, 4, 5, 6, 7, 8};
[Step #8]
						8(R)
				7(B)
		6(R)
				5(B)
4(B)
				3(B)
		2(R)
				1(B)

//testVector = { 8, 7, 6, 5, 4, 3, 2, 1};
[Step #8]
				8(B)
		7(R)
				6(B)
5(B)
				4(B)
		3(R)
				2(B)
						1(R)

Even though it’s rotated 90 degree, we can see how the data and tree look like in memory.

and we can see our code works properly.

3.2 Delete

3.2.1 Rules

So far we went over how insert works, it is slightly more complicated with delete operation. Someone might be just easily thinking “Delete operation might work properly if we use same rule as insert after disconnecting target node?“.

But here is more efficienated way.

• Rule#0: Don’t forget Rule#0 mentioned above, all routes from root to nil node should have same number of black nodes.

Let’s remind Rule#0 and take a look at below and assume that we will remove Node 3 in below tree.

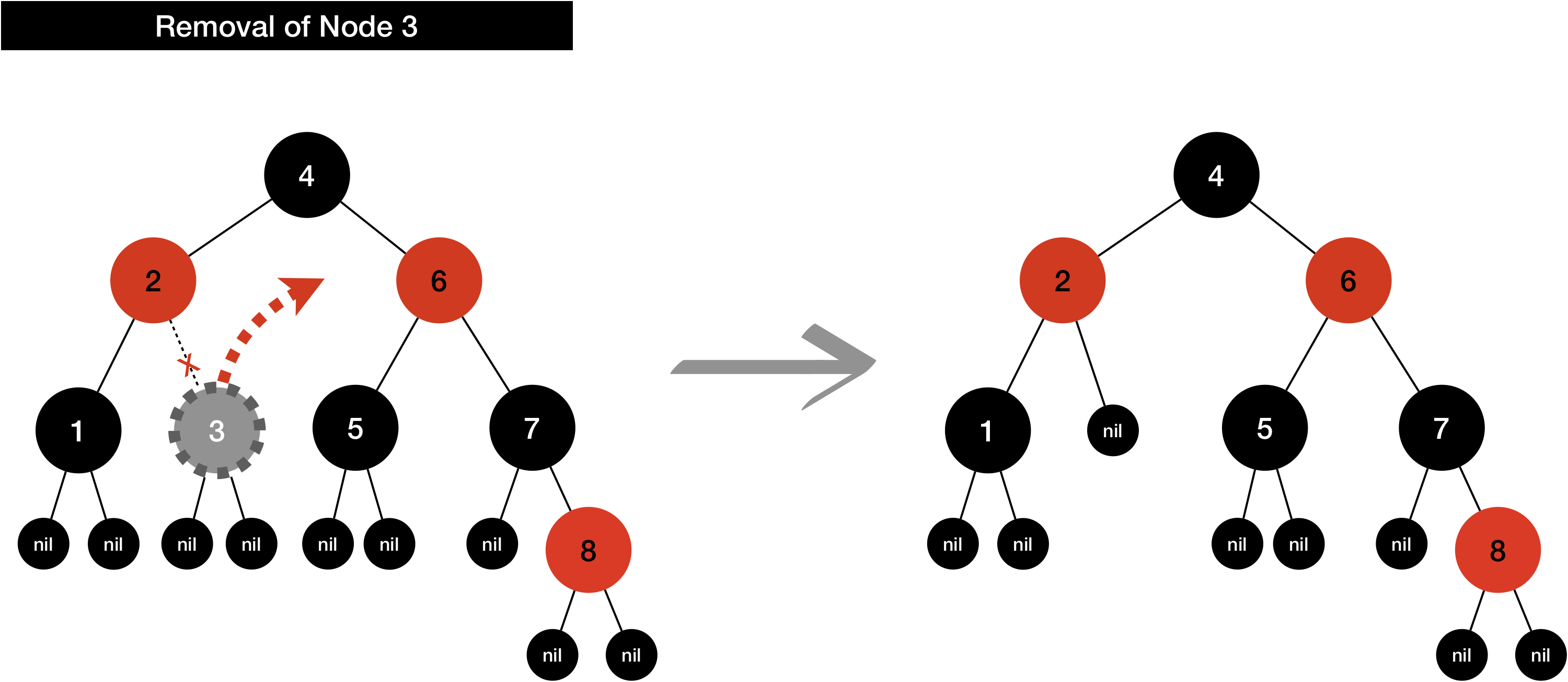
If Node 3 is removed, route from root (4) to nil node where Node 3 was placed has only 2 Black node unlike other routes, other routes still have 3 black nodes in it.

Which means balance is broken, when we can easily reach a conclusion that tree will be imbalanced if you remove Black node, because whether tree is well-balanced or not is determined by number of Black node.

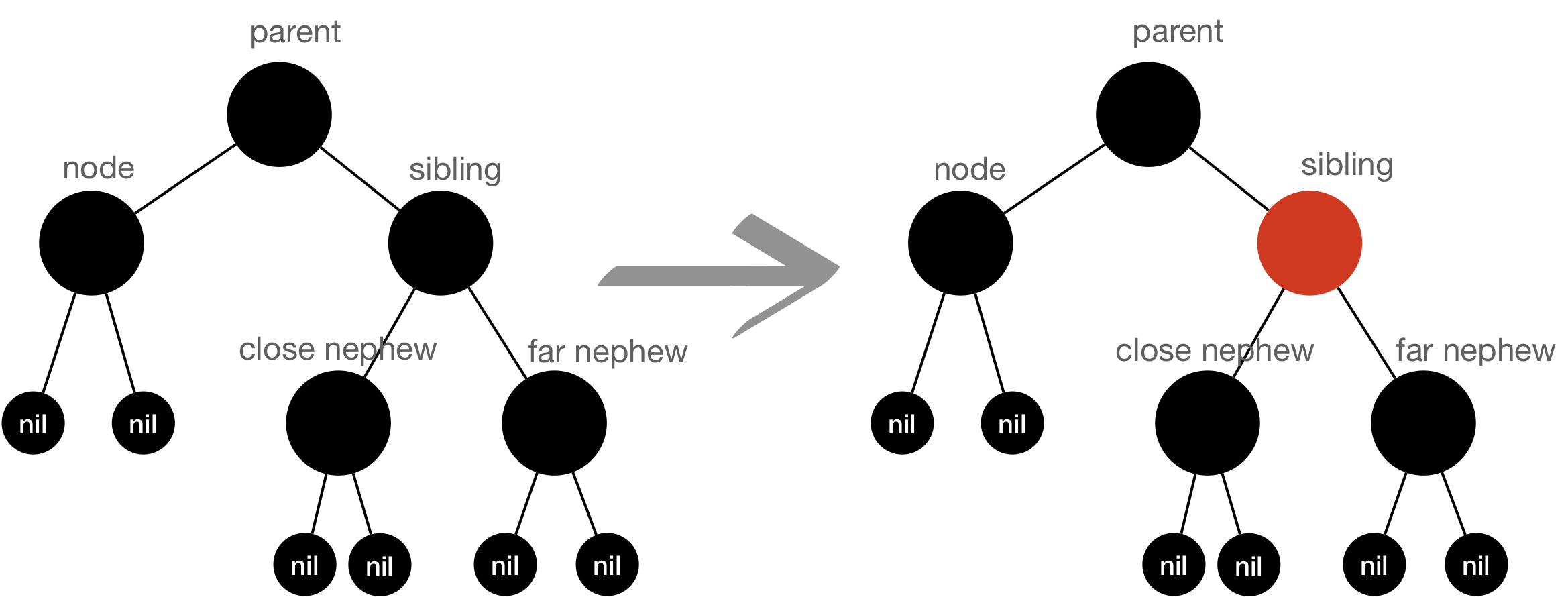
• Rule#1: Sibling node is Red, which means parent and newphews all should be black according to the insert rules.
  • if Sibling is on rightside of target(delete)
    • Color flip
      • Parent —> RED
      • Sibling —> BLACK
    • RotateLeft( Parent )

• Rule#2: Parent, Sibling, and Nephew all are BLACK
  • Color flip
    • Sibling —> RED

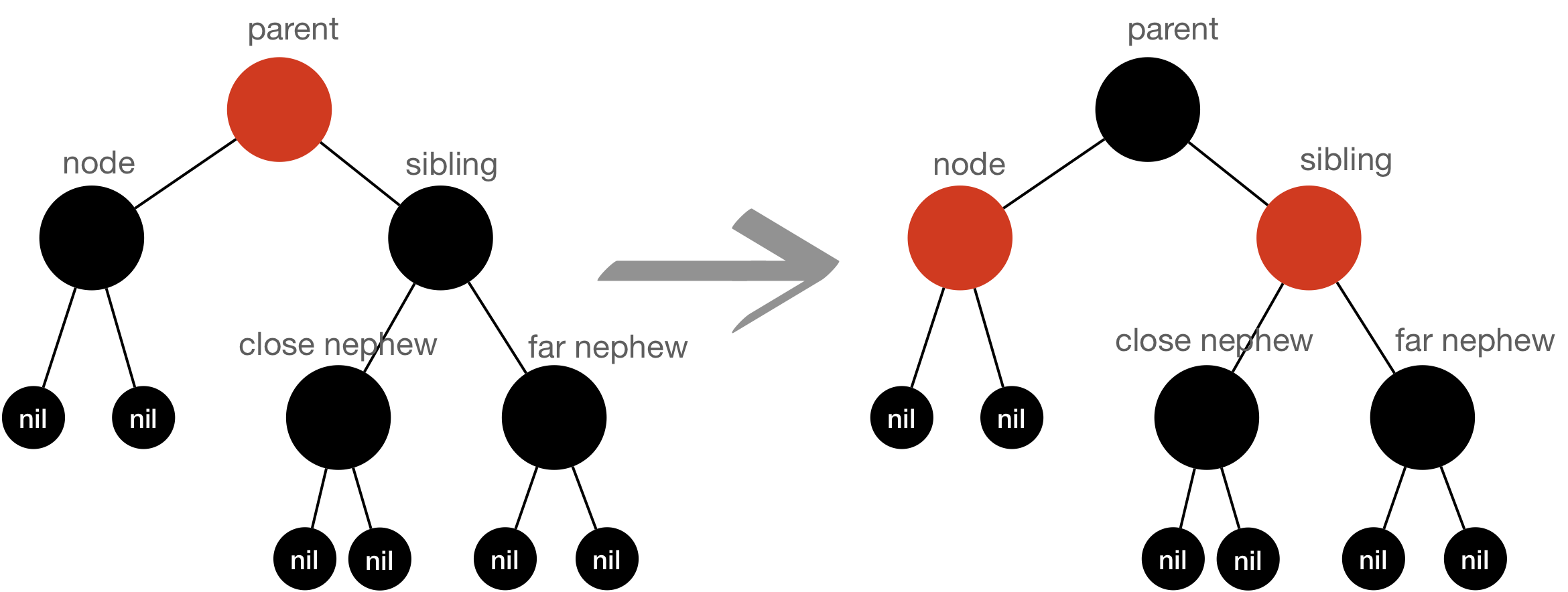
• Rule#3: All nephews are BLACK and Parent is RED, which implies me, target node, and sibling must be BLACK
  • Color flip
    • Sibling —> RED
    • Target node —> RED ( This is not required to implement as it will be anyway removed)
    • Parent —> BLACK

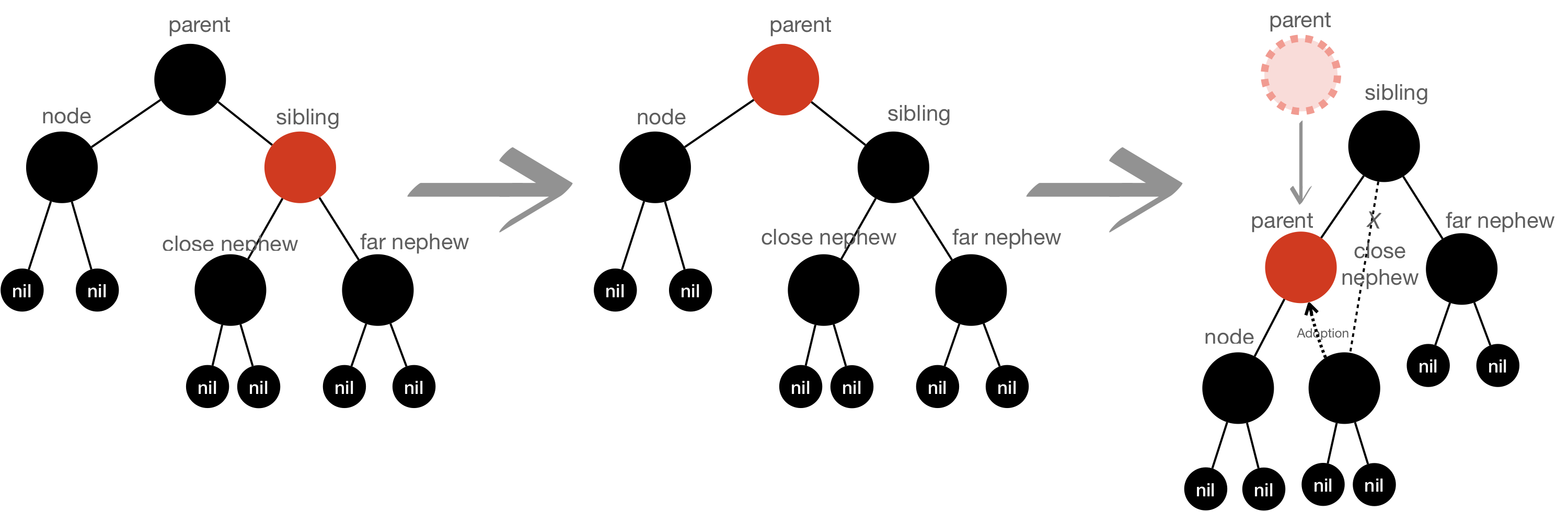
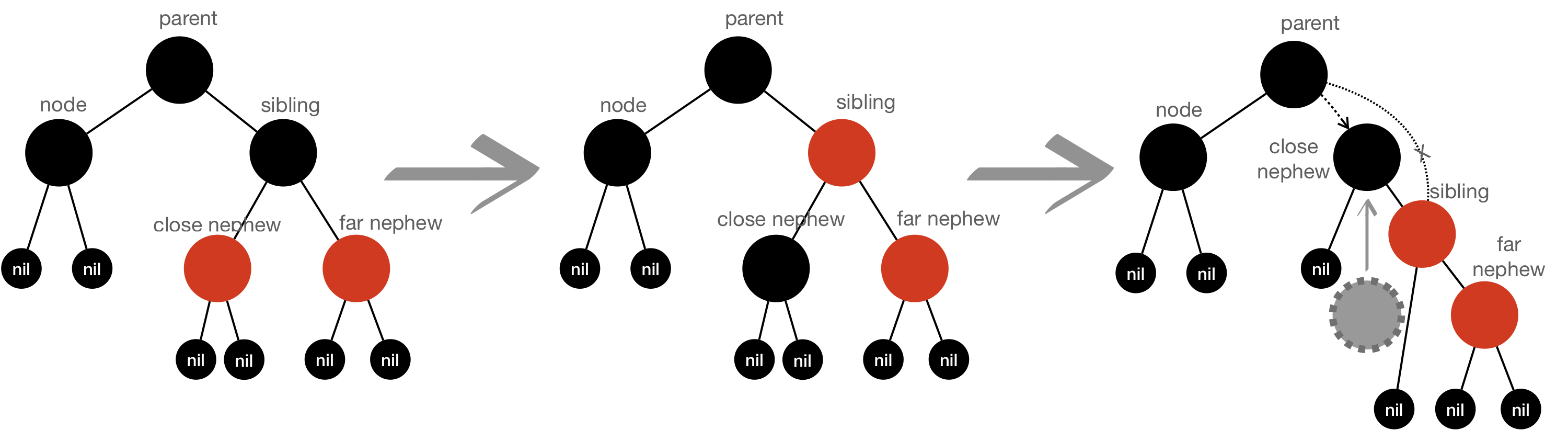
• Rule#4: Closest nephew is RED - Color flip - Closest nephew —> BLACK - Sibling —> RED - RotateRight( Sibling )

• Rule#5: Farest nephew is RED - Color flip - Parent —> BLACK - Sibling —> Inherit color of its parent - Farest nephew —> BLACK - RotateLeft( parent )

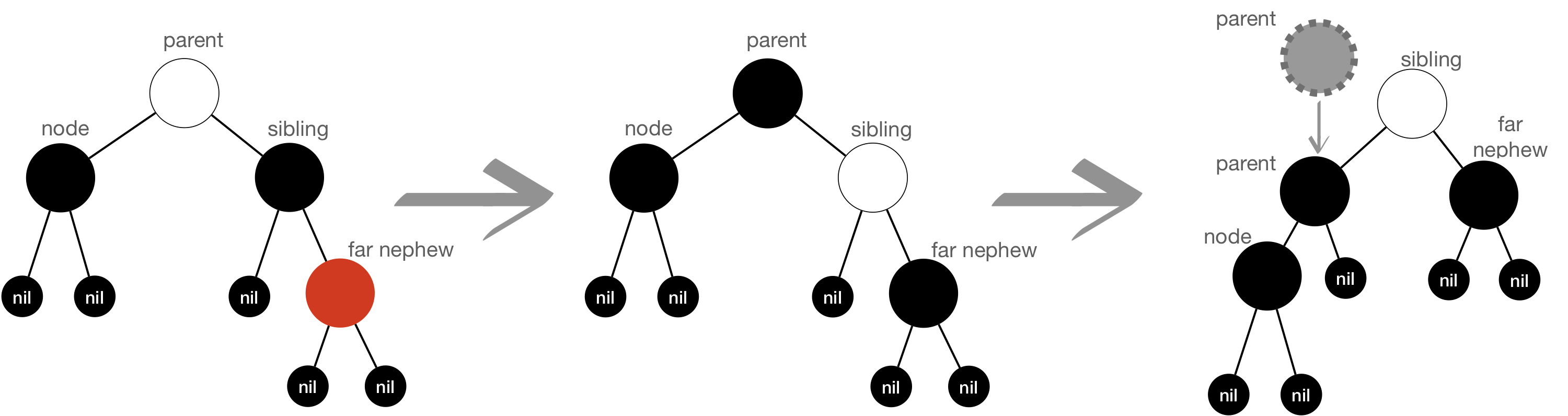
*White Node in the figure means inheritance of color

After applying above 5 rules, Please remind that node will be removed from the tree.

When you see the figure above for Rule#5, final tree looks unbalanced tree, but node, which is target node to remove, will be removed from the tree and tree is finally balanced.

Let’s illustrate how tree looks like if we remove from 1 to 8 from the tree that we have made in insert section.

3.2.2 Implementation

Okay, it is time to code!

During this session, I would change some of code of rotating functions because previously, we just delivered current target node as parameter but actual rotated node was gParent node.

During implementing remove function, I will reuse rotation function, but it requires to rotate parent of sibling. Previously, if you deliver target node as a parameter, rotation happened based on its parent, which menas gParent will be rotated. Instead of delivering target node, I will change to deliver pivot node which will be based while rotation is happening. This is an example of rotateLeft(), I just changed first line of function.

void rotateLeft(Node *node){
	//Node *parent = node->parent;
	Node *parent = node;
	Node *gParent = parent->parent;
	Node *ggParent = gParent->parent;

	if (ggParent) { //ggParent != NULL
		if (ggParent->left == gParent){ //
			ggParent->left = parent;
			parent->parent = ggParent;
		}
		else {
			ggParent->right = parent;
			parent->parent = ggParent;
		}
	}
	else { //ggParent == NULL, which means gParent == root
		root = parent;
		root->parent = NULL;
	}

	if (parent->left){ // if child of current parent exists
		//inherit
		//parent’s child will be always bigger that gParent (target of rotating)
		//that means it will be placed as a right child of new Parent
		gParent->right = parent->left;
		parent->left->parent = gParent;
	}
	else {
		gParent->right = NULL; // clear pointer
	}
	parent->left = gParent; 
	gParent->parent = parent;
}

As I changed rotate function, I had to change on __balancing() function as well, just delivered node’s parent instead of node.

void __balancing(Node *node){

…
	else {
		…
		if(node == parent->right){
			//Right-Heavy
			//rotateLeft(node);
			rotateLeft(node->parent);
		}
		else {
			//Left-Heavy
			//rotateRight(node);
			rotateRight(node->parent);
		}
	}
…
}

Now let’s implement core part. As we implemented addNode before, you can implement removeNode like below.

void removeNode(int data){
	Node *target = root;
	while(target) {
		if(target->data < data) target = target->right;
		else if(target->data > data) target = target->left;
		else break; //found!!
	}
	if(target){
		__rebalancing_for_removal(target); // rebalancing
	} else {
		printf(“Not found %d\n”, data);
	}
}

It is quite simple, removeNode will find data in the binary search, and rebalancing and remove operation will be executed once it is found.

Each of rule is defined in below code with comment.

Remove function’s operation is highly relying on existence of sibling.

For Rule#2 and Rule#3, it will break the loop if there is no sibling.

void __rebalancing_for_removal(Node *node) {
	
	while (node->color == BLACK && node != root) {
		Node *parent = node->parent;
		Node *sibling = parent->left == node ? parent->right : parent->left;
		Node *cNephew = sibling == NULL ? NULL : parent->left == node ? sibling->left : sibling->right;
		Node *fNephew = sibling == NULL ? NULL : parent->left == node ? sibling->right : sibling->left;

		if (sibling!=NULL && sibling->color == RED) {//Rule#1
			parent->color = RED;
			sibling->color = BLACK;
			
			//sibling
			if (parent->right == sibling) {
				rotateLeft(sibling);
			}
			else {
				rotateRight(sibling);
			}
		}
		else { //sibling->color == BLACK
			if (fNephew == NULL || fNephew->color == BLACK) {
				if (cNephew == NULL || cNephew->color == BLACK) {
					if (parent->color == BLACK) {//Rule#2
						if (sibling != NULL)
							sibling->color = RED;
						else
							break;
					}
					else { //Parent->color == RED,  Rule#3
						if (sibling != NULL) {
							sibling->color = RED;
							node->color = RED;
							parent->color = BLACK;
						}
						else 
							break;
						
					}
				}
				else {// cNephew->color == RED, Rule#4
					cNephew->color = BLACK;
					sibling->color = RED;

					if (parent->right == sibling) {
						rotateRight(sibling); 
					}
					else {
						rotateLeft(sibling);
					}
					
				}
			}
			else { //fNephew->color == RED //Rule#5
				sibling->color = parent->color;
				parent->color = BLACK;
				fNephew->color = BLACK;

				if (parent->right == sibling) {
					rotateLeft(sibling);
				}
				else {
					rotateRight(sibling);
				}
			}

		}

	}

	
	if (node->parent) {
		if (node->parent->left == node) {
			//inherit
			if (!node->left && !node->right) node->parent->left = NULL;
			else if (node->left) {
				node->parent->left = node->left;
				node->left->parent = node->parent;
			}
			else {
				node->parent->left = node->right;
				node->right->parent = node->parent;
			}

		}
		else {
			if (!node->left && !node->right) node->parent->right = NULL;
			else if (node->left) {
				node->parent->right = node->left;
				node->left->parent = node->parent;
			}
			else {
				node->parent->right = node->right;
				node->right->parent = node->parent;
			}
		}
	}
	else {
		root = NULL;
	}
	free(node);
}

3.2.3 Test

We can test with int vectors[8] = { 1,2,3,4,5,6,7,8 }; from inserting the items to removing the items in order.

int main() {
	int vectors[8] = { 1,2,3,4,5,6,7,8 };
	//int vectors[8] = { 8,7,6,5,4,3,2,1};
	printf("=== Red-Black Tree Test ===\n");
	for (int i = 0; i < 8; i++) {
		getchar();
		insertNode(vectors[i]);
		system("cls");
		printf("Insert [Step #%d]\n", i + 1);
		displayTree(root);
	}

	for (int i = 0; i < 8; i++) {
		getchar();
		removeNode(vectors[i]);
		system("cls");
		printf("Remove [Step #%d]\n", i + 1);
		displayTree(root);
	}
	return 0;
}

Remove [Step #1]
                        8(R)
                7(B)
        6(R)
                5(B)
4(B)
                3(R)
        2(B)

Remove [Step #2]
                8(R)
        7(B)
6(B)
                5(R)
        4(B)
                3(R)

Remove [Step #3]
                8(R)
        7(B)
6(B)
                5(R)
        4(B)

Remove [Step #4]
        8(B)
7(B)
        6(B)
                5(R)

Remove [Step #5]
        8(B)
7(B)
        6(B)

Remove [Step #6]
8(B)
        7(R)

Remove [Step #7]
8(B)

Remove [Step #8]

3.3 Overall code

I share overall code for the red-black tree that we implemented above.

If I made wrong code, feel free to share your input in comment section. Hope that this post helps you to understand Red-Black Tree.

#include <stdio.h>
#include <stdlib.h>
#include <windows.h>

enum COLOR {
	RED, BLACK
};

typedef struct _node {
	int data;
	COLOR color;
	struct _node *left, *right, *parent;
} Node;
void __balancing(Node *node);
void rotateLeft(Node *node);
void rotateRight(Node *node);
void __rebalancing_for_removal(Node *node);
void displayTree(Node *next);

Node * getNewNode(int data) {
	Node * newNode = (Node*)malloc(sizeof(Node));
	newNode->color = RED;
	newNode->data = data;
	newNode->left = NULL;
	newNode->right = NULL;
	newNode->parent = NULL;

	return newNode;
}

Node *root = NULL;

void removeNode(int data) {
	//search node
	Node *target = root;

	while (target) {
		if (target->data < data) target = target->right;
		else if (target->data > data) target = target->left;
		else break;
	}

	if (target) {
		__rebalancing_for_removal(target);//rebalancing		
	}
	else {
		printf("Not found %d\n", data);
	}
}

void __rebalancing_for_removal(Node *node) {
	
	while (node->color == BLACK && node != root) {
		Node *parent = node->parent;
		Node *sibling = parent->left == node ? parent->right : parent->left;
		Node *cNephew = sibling == NULL ? NULL : parent->left == node ? sibling->left : sibling->right;
		Node *fNephew = sibling == NULL ? NULL : parent->left == node ? sibling->right : sibling->left;

		if (sibling!=NULL && sibling->color == RED) {//Rule#1, if (fNephew->color == BLACK && parent->color == BLACK)
			parent->color = RED;
			sibling->color = BLACK;
			
			//sibling
			if (parent->right == sibling) {
				rotateLeft(sibling);
			}
			else {
				rotateRight(sibling);
			}
		}
		else { //sibling->color == BLACK
			if (fNephew == NULL || fNephew->color == BLACK) {
				if (cNephew == NULL || cNephew->color == BLACK) {
					if (parent->color == BLACK) {//Rule#2
						if (sibling != NULL)
							sibling->color = RED;
						else
							break;
					}
					else { //Parent->color == RED,  Rule#3
						if (sibling != NULL) {
							sibling->color = RED;
							node->color = RED;
							parent->color = BLACK;
						}
						else 
							break;
						
					}
				}
				else {// cNephew->color == RED, Rule#4
					cNephew->color = BLACK;
					sibling->color = RED;

					if (parent->right == sibling) {
						rotateRight(sibling); 
					}
					else {
						rotateLeft(sibling);
					}
					
				}
			}
			else { //fNephew->color == RED //Rule#5
				sibling->color = parent->color;
				parent->color = BLACK;
				fNephew->color = BLACK;

				if (parent->right == sibling) {
					rotateLeft(sibling);
				}
				else {
					rotateRight(sibling);
				}
			}

		}

	}

	
	if (node->parent) {
		if (node->parent->left == node) {
			//inherit
			if (!node->left && !node->right) node->parent->left = NULL;
			else if (node->left) {
				node->parent->left = node->left;
				node->left->parent = node->parent;
			}
			else {
				node->parent->left = node->right;
				node->right->parent = node->parent;
			}

		}
		else {
			if (!node->left && !node->right) node->parent->right = NULL;
			else if (node->left) {
				node->parent->right = node->left;
				node->left->parent = node->parent;
			}
			else {
				node->parent->right = node->right;
				node->right->parent = node->parent;
			}
		}
	}
	else {
		root = NULL;
	}
	free(node);
}
void insertNode(int data) {
	Node *newNode = getNewNode(data);
	Node *parent = NULL;
	Node **current = &root;

	while (*current) {
		parent = *current;

		if ((*current)->data < data) current = &(*current)->right;
		else if ((*current)->data > data) current = &(*current)->left;
		else return;
	}
	newNode->parent = parent;
	*current = newNode;
	if (parent == NULL) {
		newNode->color = BLACK;
	}

	__balancing(newNode);

}


void __balancing(Node *node) {
	
	while (node->parent != NULL  //target node == root
		&& node->parent->color == RED && node->color == RED) { // 
		Node *gParent = node->parent->parent;
		Node *parent = node->parent;
		Node *uncle = gParent->left;
		if (parent == gParent->left) { //uncle == right
			uncle = gParent->right;
		}
		
		//Rule#3
		if (uncle != NULL && uncle->color == RED) { //Uncle exists and Uncle is Red
			//Color flip only

			parent->color = BLACK;
			uncle->color = BLACK;
			gParent->color = RED;
			
		}
		else { // Rule#4, uncle is NULL or uncle is black
			//Color flip
			
			gParent->color = RED;
			parent->color = BLACK;

			if (node == parent->right) { //Uncle is black and node is right
				//Right-Heavy
				//Rotate
				
				rotateLeft(node->parent);
			}
			else {
				//Left-Heavy
				//Rotate
				
				rotateRight(node->parent);
			}
			
		}

		root->color = BLACK; //Rule#1
		node = gParent;

	}
}

void rotateLeft(Node *node) {//node --> target
	Node *parent = node;
	Node *gParent = parent->parent;
	Node *ggParent = gParent->parent;


	if (ggParent) { //ggParent != Null 
		if (ggParent->left == gParent) {
			ggParent->left = parent;
			parent->parent = ggParent;
		}
		else {
			ggParent->right = parent;
			parent->parent = ggParent;
		}
	}
	else { //ggParent == NULL means gParent == root
		root = parent;
		root->parent = NULL;

	}


	if (parent->left) {
		//inherit
		gParent->right = parent->left;
		parent->left->parent = gParent;

	}
	else {
		gParent->right = NULL;
	}
	parent->left = gParent;
	gParent->parent = parent;
}

void rotateRight(Node *node) { //node --> target
	Node *parent = node;
	Node *gParent = parent->parent;
	Node *ggParent = gParent->parent;

	if (ggParent) {
		if (ggParent->left == gParent) {
			ggParent->left = parent;
			parent->parent = ggParent;
		}
		else {
			ggParent->right = parent;
			parent->parent = ggParent;
		}
	}
	else {
		root = parent;
		root->parent = NULL;

	}

	if (parent->right) {
		//inherit
		gParent->left = parent->right;
		parent->right->parent = gParent;
	}
	else {
		gParent->left = NULL;
	}

	parent->right = gParent;
	gParent->parent = parent;
}
void displayTree(Node *next) {

	if (next == NULL) return;
	static int indent = -1;
	
	++indent;

	displayTree(next->right);
	for (int i = 0; i < indent; i++) printf("\t");
	printf("%d(%c)\n", next->data,next->color ? 'B': 'R');
	displayTree(next->left);
	--indent;
}

int main() {
	int vectors[8] = { 1,2,3,4,5,6,7,8 };
	//int vectors[8] = { 8,7,6,5,4,3,2,1};
	printf("=== Red-Black Tree Test ===\n");
	for (int i = 0; i < 8; i++) {
		getchar();
		insertNode(vectors[i]);
		system("cls");
		printf("Insert [Step #%d]\n", i + 1);
		displayTree(root);
	}

	for (int i = 0; i < 8; i++) {
		getchar();
		removeNode(vectors[i]);
		system("cls");
		printf("Remove [Step #%d]\n", i + 1);
		displayTree(root);
	}
	return 0;
}

Try to code it by yourself!

4. Conclusion

We have talked about Red-Black Tree , it has quite complicated rules, but you can get more benefit than complexity of the code.

It is always good to try implementing existing good tree by yourself, which improves your understanding of the algorithm as well as giving some insperation when you need to design some algorithm.

I would suggest other type of auto balancing tree such as AVL Tree, 2-3 Tree, 2-3-4 Tree, B Tree, B+ Tree, B* Tree that I mentioned at the beginning of the post.

Now I implemented that each of node has fixed type of data in it, i.e.) int data. In other language, c++,typescript, go and etc.. that have generic, can be solving this problem easier. However C also has the solution for this that we can separate data type and node type.

Let’s deep dive in generic linked list next time, and think how we can implement generic in C and how we can apply this to Red-Black Tree.

See you soon,

Happy coding!

Regards,

Jeesub