Fundamental of Binary Tree & Binary Search Tree
1. Introduction of Tree
Tree is one of basic concepts of data structure, which is very commonly used in computer science. With tree, we were able to implement File system, Database indexing, Pattern matching for the strings, Auto completion, Network routing and game development easily.
However, why it’s called Tree?
It’s literally looking tree, but up-side down one.
Let’s imagine how Tree looks like.

Fig.1 Nature of Tree
There’s root at the bottom, and multiple braches with leaves at the top.
if we make a tree with nodes, this is how we can map with.
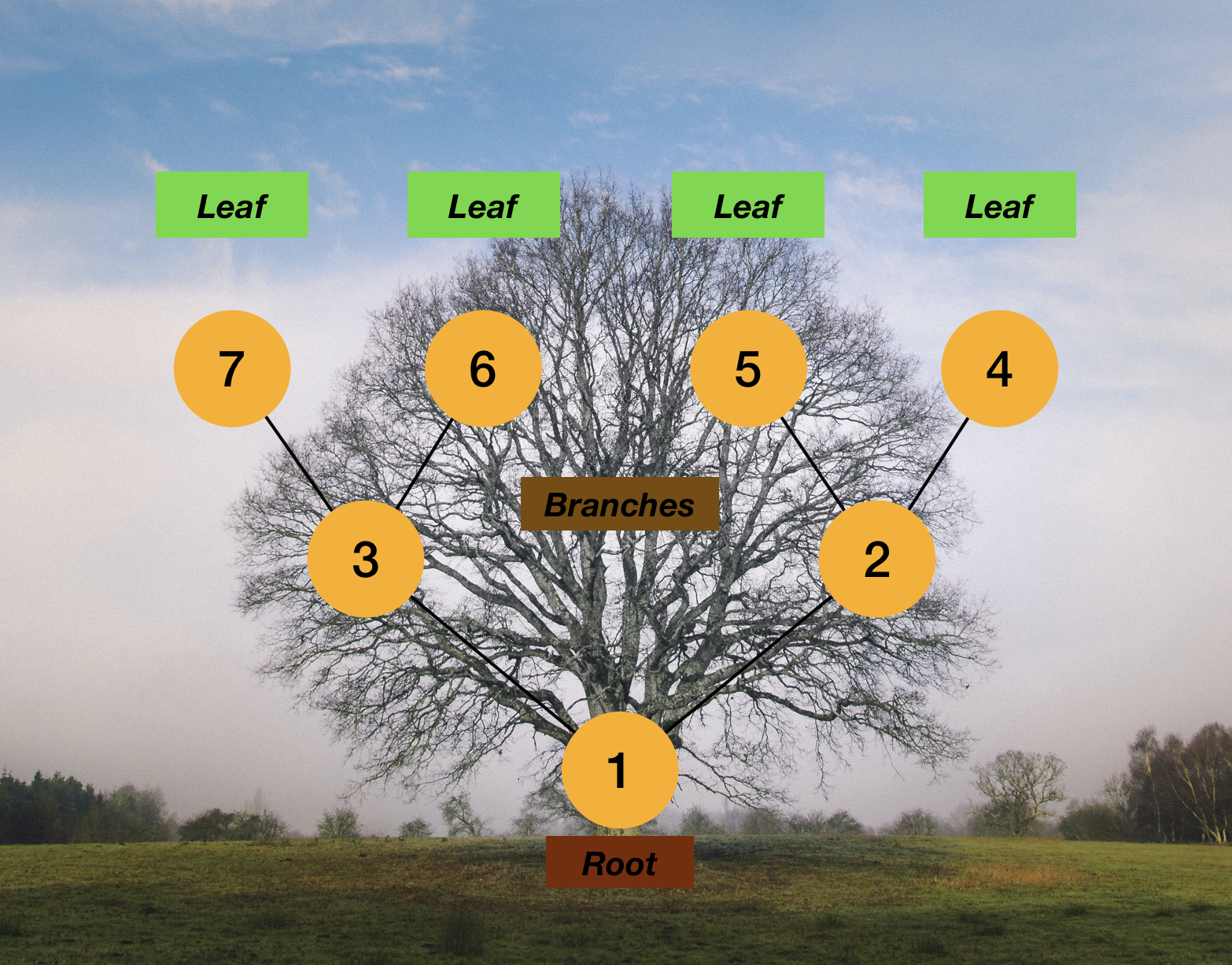
Fig.2 Real tree vs the tree data structure in computer science
Today, we will talk about what the Tree is in computer science with definition, terms and implementation.
1.1 Terms
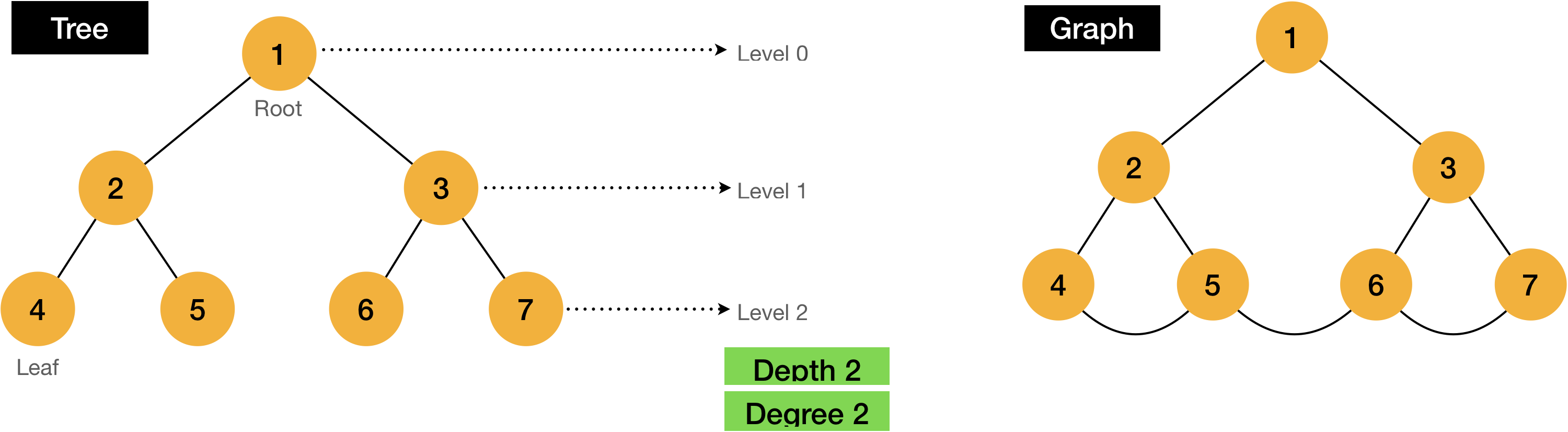
- Node / Vertex: Each item, circles in the figure
- Edge: Connected line between Node and Node
- Root Node: Top most node, Acestor of every node
- Leaf Node: Nodes which don’t have child node, terminal node
- #4, 5, 6, 7 nodes in the figure
- Level: Hierarchy level of tree
- Depth: Maximum level of tree
- Degree: Maximum edge from the node
- 2 in the figure, which is binary tree
1.2 Definition of Tree
Path from the node to the another one is only one.
Otherwise, it’s called graph.
Starting from the root, all nodes should be connected, but has only one path from the one to the others.
1.3 Implementation
1.3.1 Initialization
In C Lang, every struct should be declared with struct keyword,
typedef is used to declare user-defined type of data, and this is how typical C programmers are writing.
typedef struct _node{
int data; // user data which will be stored in the each node
struct _node *left; // pointer which is pointing left child
struct _node *right; // right child
} Node; // naming `struct _node`
Node *root = NULL; //declaration of root node with pointer
Above is an example of initialization of binary tree in C, you can see root node is also declared as pointer, which means there will be no actual space until you assign some space for the root.
(Of course, you are assigning memory for the pointer which is pointing struct _node)
While writing the initiation code, we can also quickly think how we can create new node?
We can easily think that new_data function can get a data, and we can assign some memory for the new node with malloc, and initiate the data with the given and left and right with NULL value.
Node* new_node(int data){
Node *node = (Node*)malloc(sizeof(Node));
node->data = data;
node->left = NULL;
node->right = NULL;
return node;
}
1.3.2 Insertion
Let’s remind how tree looks like.
It must be starting from the root, which means data should be filled out from the root.
We can note down the basic concept of the tree what we are trying to implement first, and implement it based on the requirement.
1. Data should be filled out from the root
2. insert_data function will just see `current` node if `root` is not empty
3. Position (Left or Right) should be delivered as one of parameters
Let’s go through the first requirement.
- Data should be filled out from the root, no matter what
currentnode is delivered as an parameter
This requirement is quite simple and straightforward.
We can just create new node and make rootpointer points new node if it’s NULL

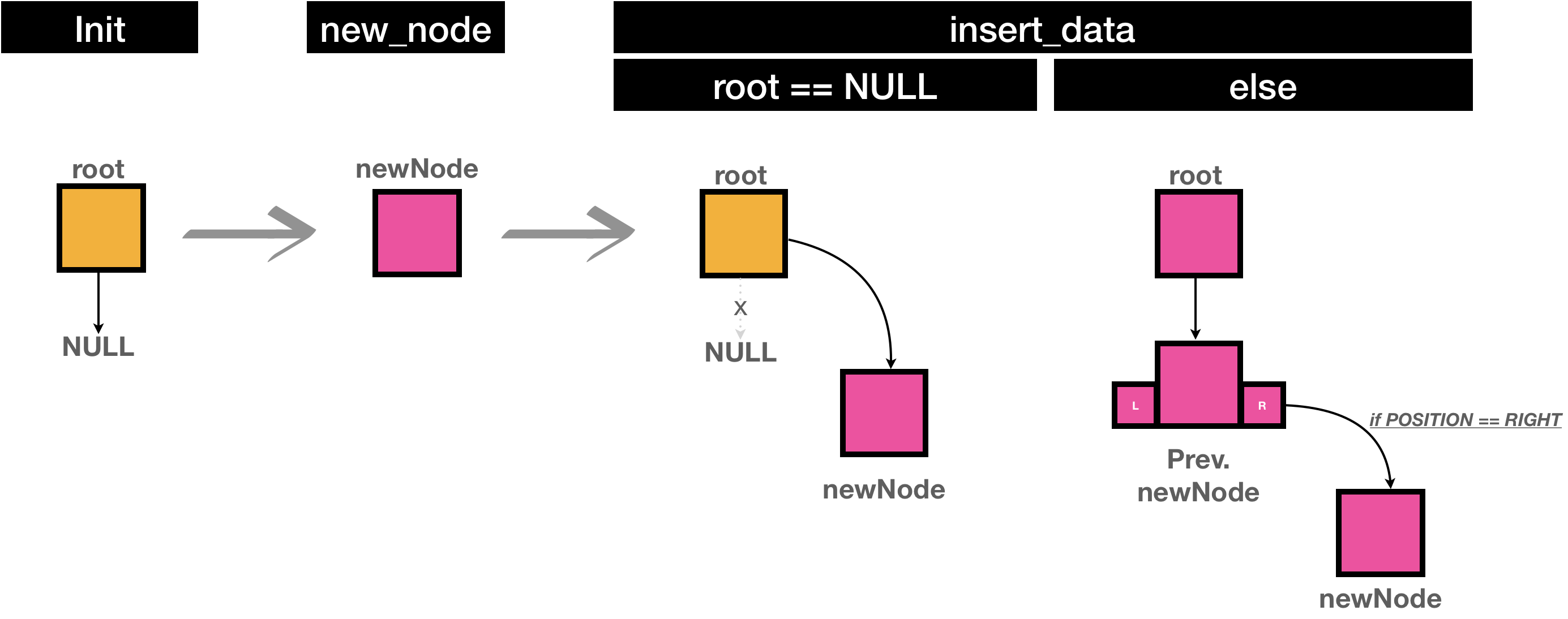
void insert_data(int data) {
Node* newNode = new_node(data);
if (root == NULL){
root = newNode;
}
}
Now, data should be filled out from the root if root is pointing NULL
- insert_data function will just see
currentnode ifrootis not empty
Now the second requirement is the case that root is not empty.
As you can see that it requires current node information, function should support receiving current node pointer as a parameter.
We can revise the function as below.
void insert_data(int data, Node *current){
Node* newNode = new_node(data);
if (root == NULL){
root = newNode;
return; // once root is filled out, this function no longer needs to be working more
}
current = newNode;
}
Is this what requirement intented? So far, there seems to be no problem. Above code is literally working as requirement required, but still requirement itself is unclear.
Let’s move on to the last requirement and see if some clarification is needed.
- Position (Left or Right) should be delivered as one of parameters
Position information is supposed to be provided, so that insert_data function should follow where, left or right, the user of this function wants to insert.
You can use enum to define position flag intead of just using 0 or 1 for the code readability.
typedef enum {
LEFT, RIGHT
} POSITION;
void insert_data(int data, Node *current, POSITION pos){
Node* newNode = new_node(data);
if (root == NULL){
root = newNode;
return; // once root is filled out, this function no longer needs to be working more
}
//current = newNode;
if(pos == LEFT) {
current->left = newNode;
} else {
current->right = newNode;
}
}
And you can add position checking logic instead of assigning newNode to current pointer, so that newNode will be assigned as one of children of current node.
So far, everything seems to be good except for the second requirement.
Let’s revise the requirement to make it clear.
insert_data function will just seecurrentnode ifrootis not emptyinsert_datafunction will refer tocurrentnode info and assignnewNodeto proper location with thepositioninformation from the following requirement
we can simply describe how the written code works.
Alright, it’s time to test. if we implement the code correctly, below tree can be made with the code in the main function below.
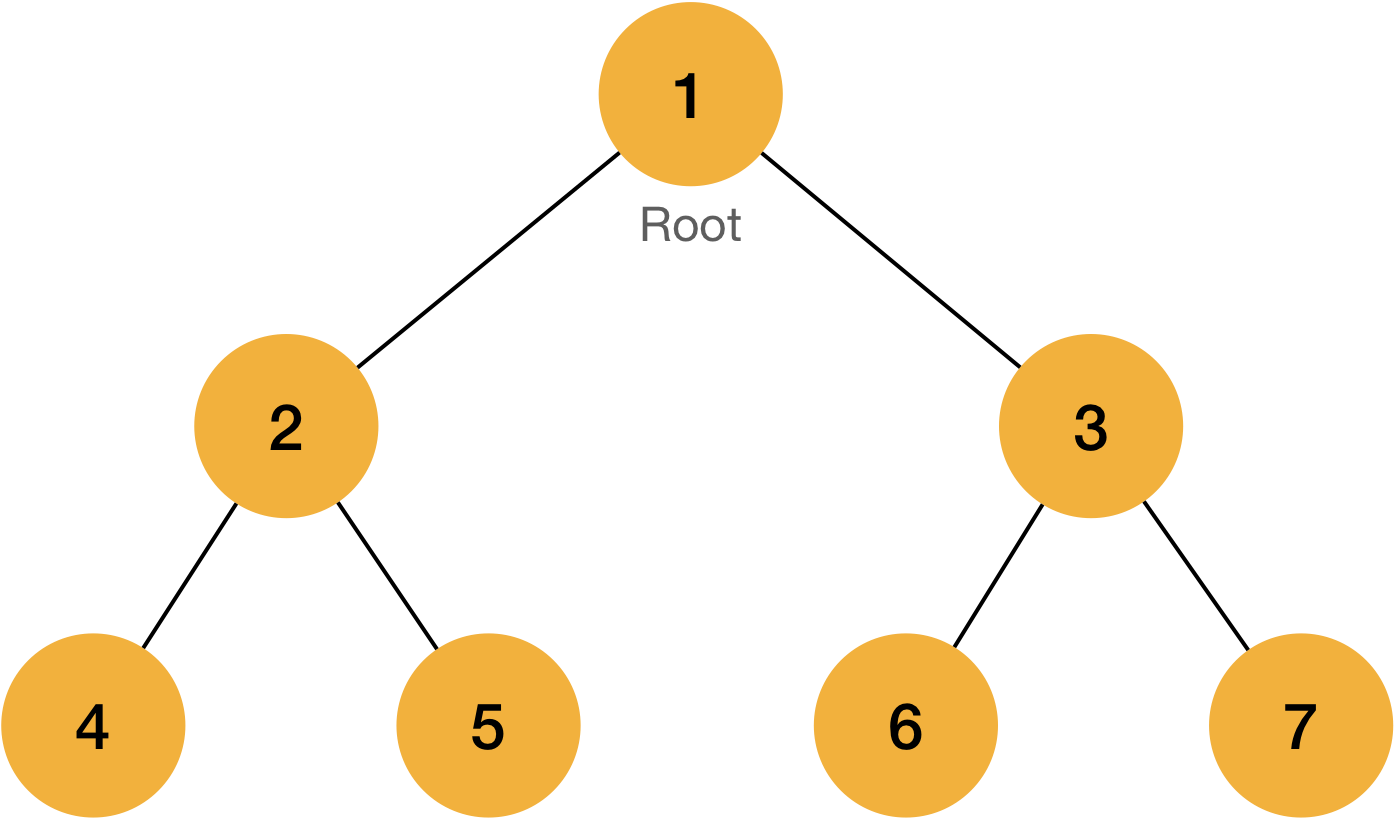
int main(){
insert_data(1, root, LEFT);
insert_data(2, root, LEFT);
insert_data(3, root, RIGHT);
insert_data(4, root->left, LEFT);
insert_data(5, root->left, RIGHT);
insert_data(6, root->right, LEFT);
insert_data(7, root->right, RIGHT);
return 0;
}
For the first insertion, no matter what value is delivered through pos parameter, it will be ignored as root is empty.
It seems that there is no problem on insertion part. Then, how can we check if each of values and pointers are in the certain node with tree shade what we intented properly?
Let’s explore more on Traverse part.
1.3.3 Tree order traverse
Tree has uni-direction structure, which means parent node only can access children node.
You can easily understand what it means as our Node has no Node *parent.
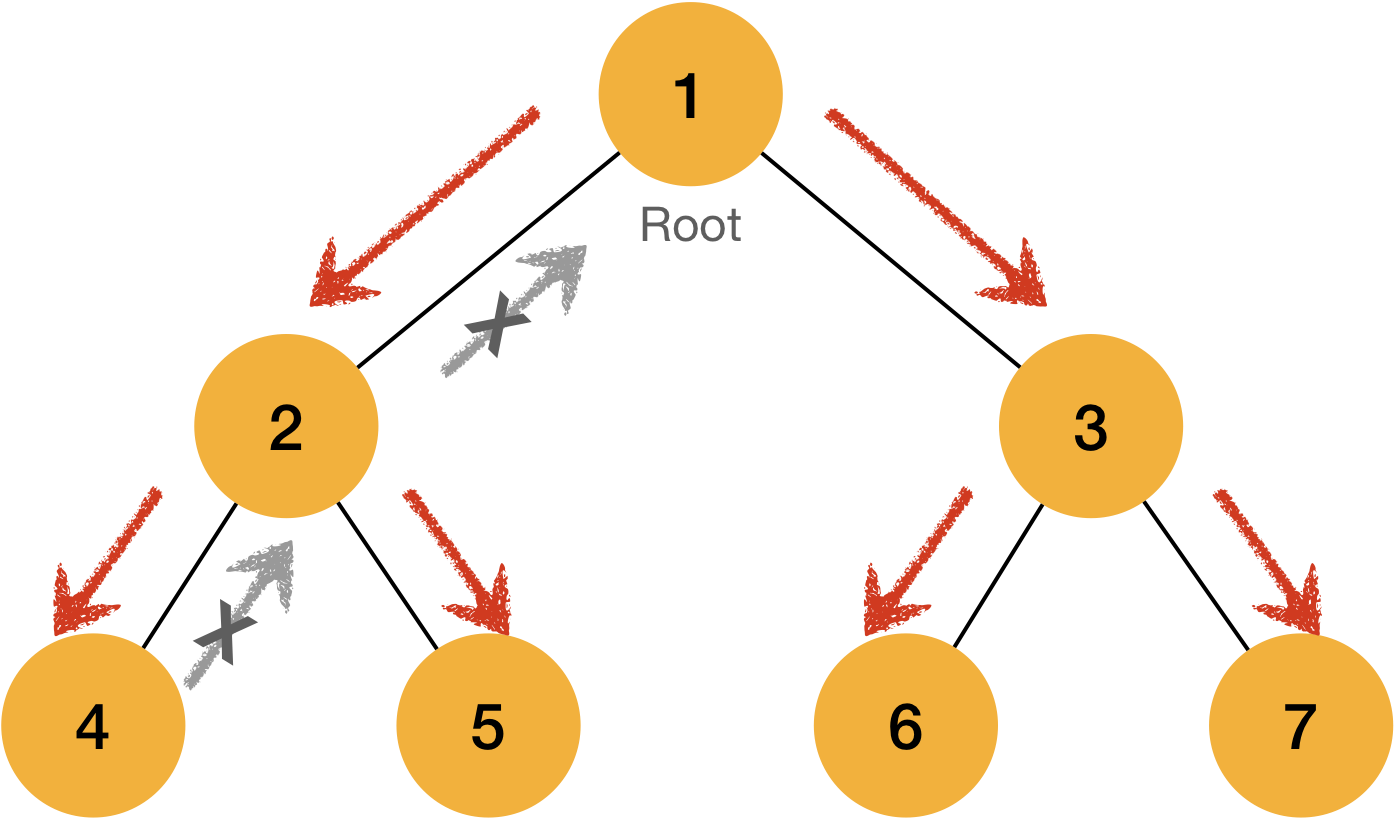
Then, how can we traverse the tree?
There are three types of traverse strategy, which are divided by when the root node will be traversed.
- Pre order traverse:
rootwill be the first - In order traverse:
rootwill be the middle of the traverse - Post order traverse:
rootwill be the last
Let’s take a look at the three way to traverse the tree below.
1.3.3.1 Pre order traverse
Pre order traverse is the strategy to traverse the tree root -> left -> right order.
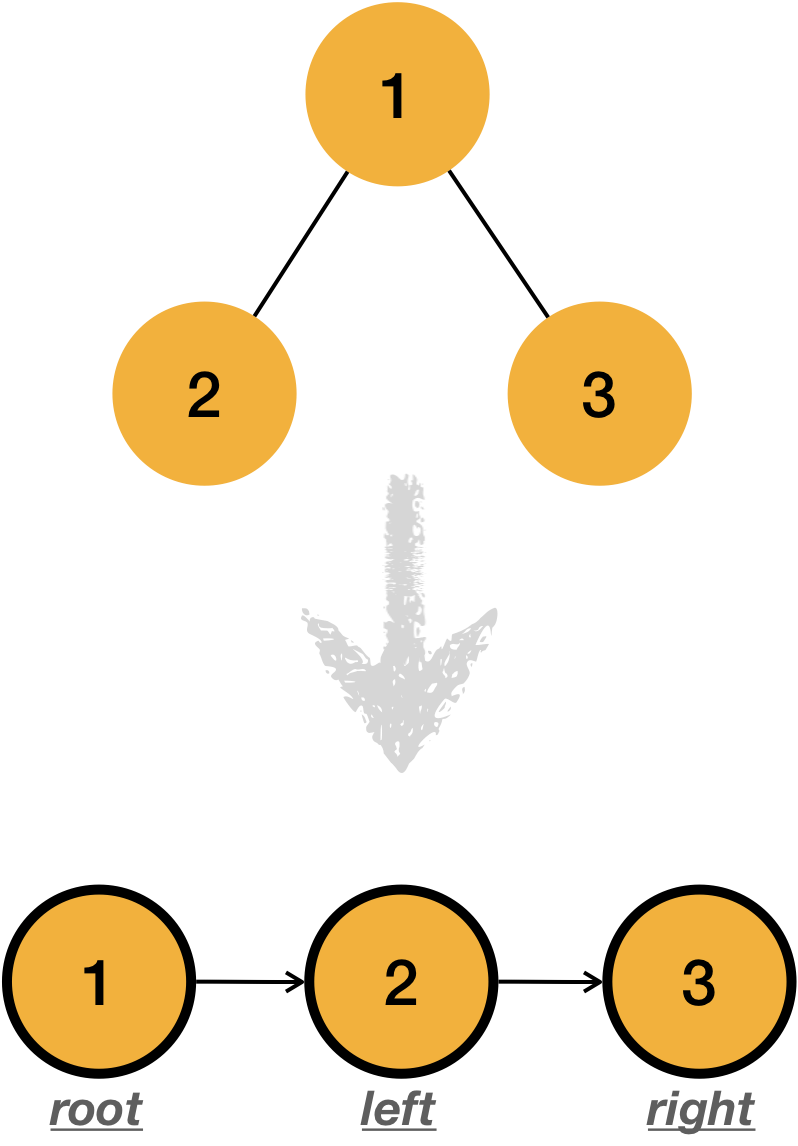
Let’s make a pre order traverse code.
void pre_order_traverse(Node *node) {
if (node == NULL) return;
printf(“%d ”,node->data);
pre_order_traverse(node->left);
pre_order_traverse(node->right);
}
Traverse looks quite simple as you can see above. Let’s quickly go over the code line by line,
- Certain node will be given as parameter, traverse will be started from that point.
- if given node is pointing
NULL, function will be finished. - Check
node’s data which will be root (1 will be printed in above example ) - Recursively check the nodes until function is finished by Step#2 above
- Left node will be checked
- Right node will be checked
1.3.3.2 In order traverse
In order traverse is the strategy to traverse the tree left -> root -> right order.
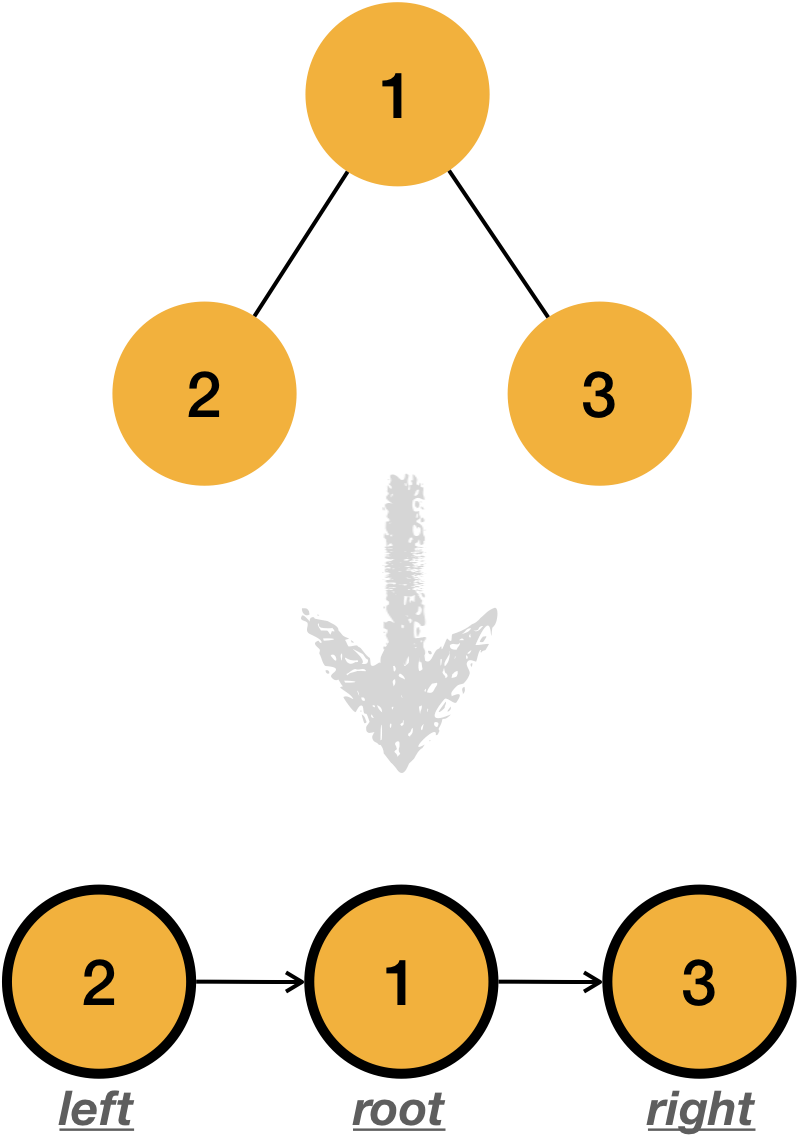
In a same way, In order traverse can be implemented like below.
void in_order_traverse(Node *node) {
if (node == NULL) return;
pre_order_traverse(node->left);
printf(“%d ”,node->data);
pre_order_traverse(node->right);
}
1.3.3.3 Post order traverse
Post order traverse is the strategy to traverse the tree from left -> right -> root order.
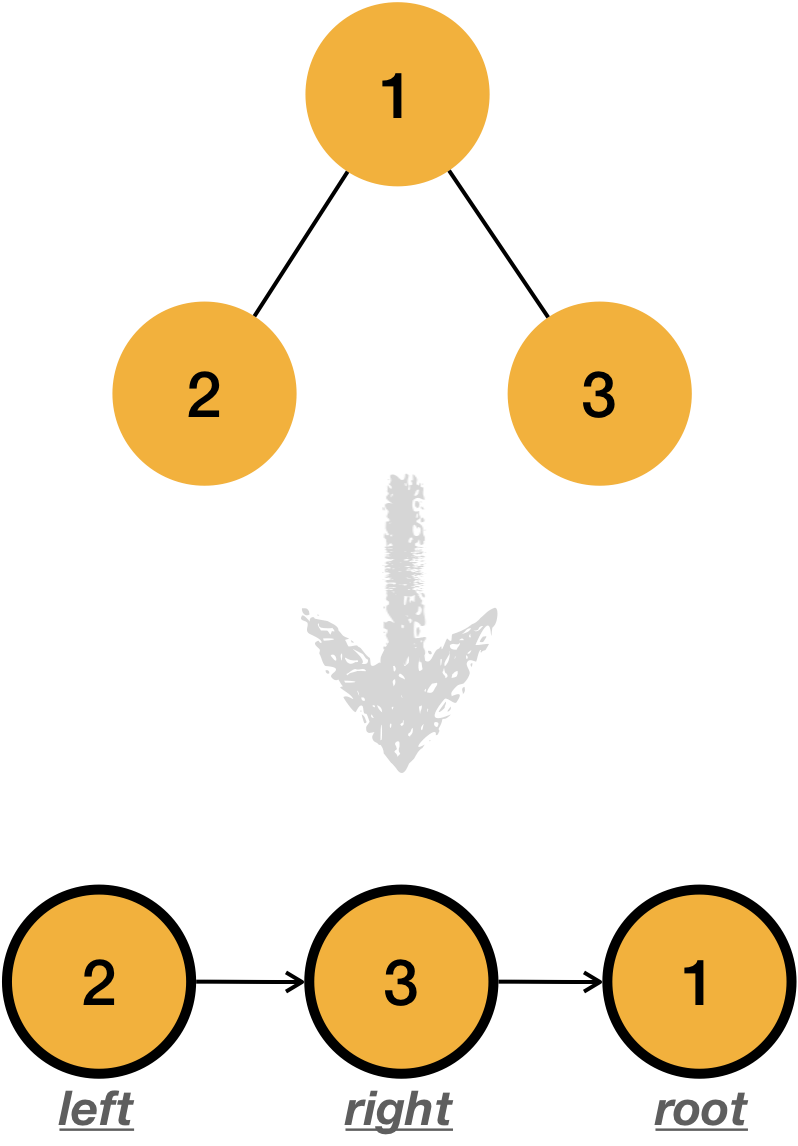
The same applies to post order traverse.
void post_order_traverse(Node *node) {
if (node == NULL) return;
pre_order_traverse(node->left);
pre_order_traverse(node->right);
printf(“%d ”,node->data);
}
Important thing to remember is, “When will the root node be traversed”
With this tree order traverse section, you are able to print and verify the insert_data function if it works as intented.
Please refer to the expectation versus outputs below.
int main(){
insert_data(1, root, LEFT);
insert_data(2, root, LEFT);
insert_data(3, root, RIGHT);
insert_data(4, root->left, LEFT);
insert_data(5, root->left, RIGHT);
insert_data(6, root->right, LEFT);
insert_data(7, root->right, RIGHT);
pre_order_traverse(root);
// expectation: 1 2 4 5 3 6 7
in_order_traverse(root);
// expectation: 4 2 5 1 6 3 7
post_order_traverse(root);
// expectation: 4 5 2 6 7 3 1
return 0;
}
2. Introduction of Binary Search Tree
In terms of data structure, we need to consider the proper data structure from the wel-fit with data perspective as well as efficient structure for the search point of view.
We have gone over what the tree is, but the code that we implemented above for the tree is not enough to use for data search. Because it needs to traverse every single node to find what user wants.
Binary search tree is well-known as fast searchable data structure. Let’s talk more detail on how it looks like and how it works.
2.1 How it looks like
You can see the binary keyword from the title, Binary search tree is tree and has binary children only.
What does
binarymean?
Binary is just 0 or 1, which can describe two status.
What does
binarymean in the tree then?
It means that tree node has only tree children.
However, there were only two nodes when we studied about the tree in previous section?
Tree can have children as many as implemented. In previous section, we just discussed about the node which has only two nodes, left and right. But it can be more than 2, i.e.) left, middle, right or so on.
Okay, then Binary search tree what you are going to describe here will be the same as you mentioned in previous section?
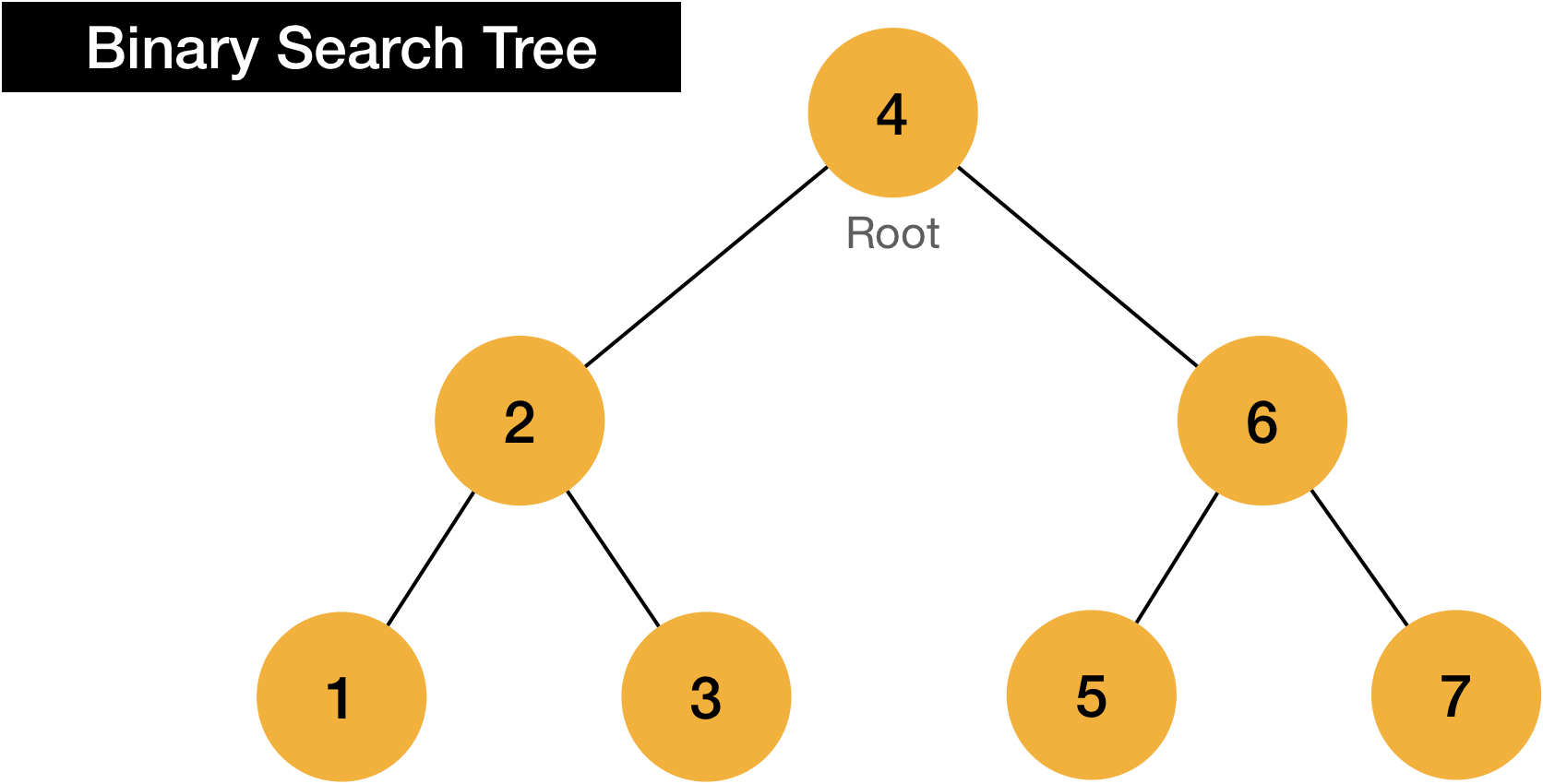
Yes, It’s completely same shape of tree, but there is important rule to make it searchable fast.
Here is difference between just binary tree versus binary search tree what we are going to talk.
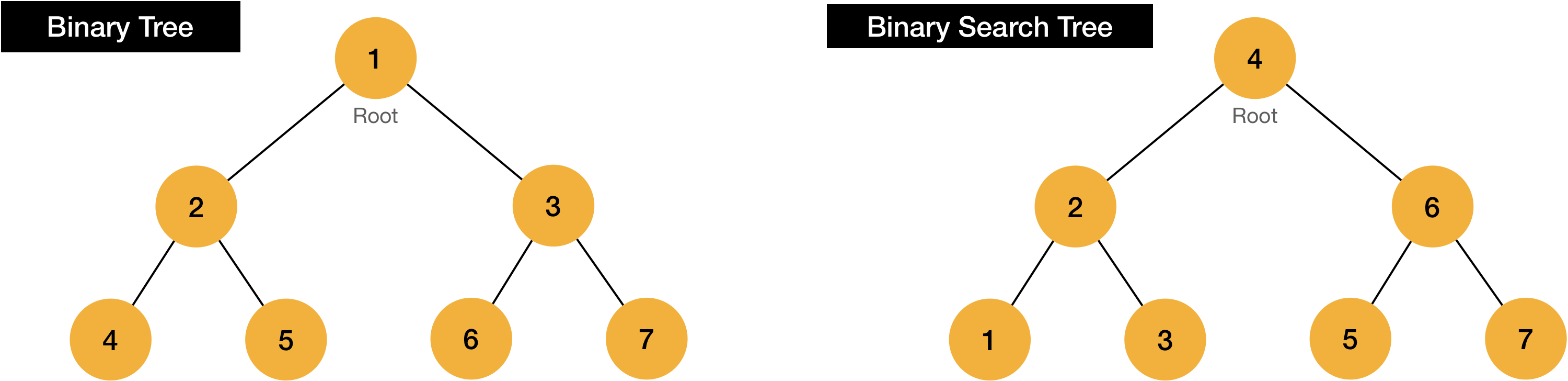
Can you easily distinguish what the difference is?
Shape of tree is just totally same. However, each node’s value is placed in different way.
Let’s deep dive in to this on How it works section.
2.2 How it works
Binary Search Tree also has quite simple and straightforward rule.
- When there is
newNode’s data, it should be assigned on the left side of parent node if the value is smaller than parent’s - Otherwise, it should be assigned on its right side. (if
newNode’s data is bigger than parent) ``
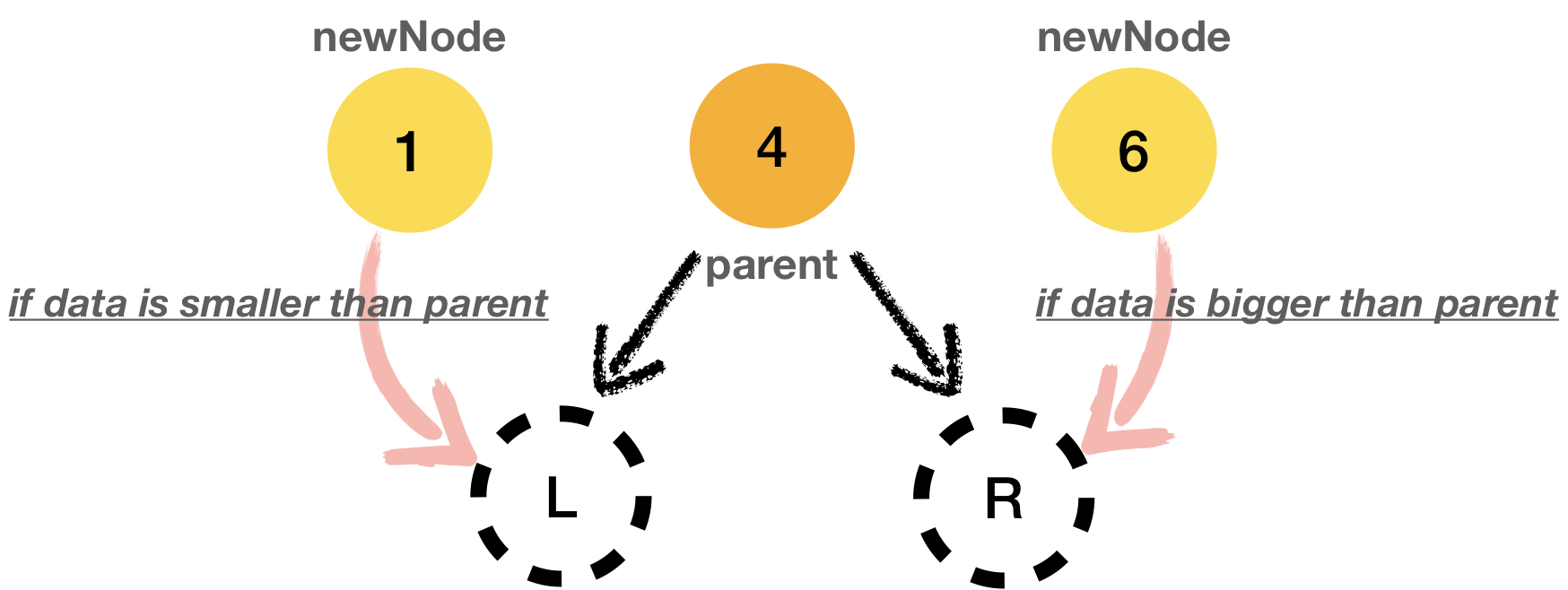
With above rule, values in tree can be stored in the tree like below.
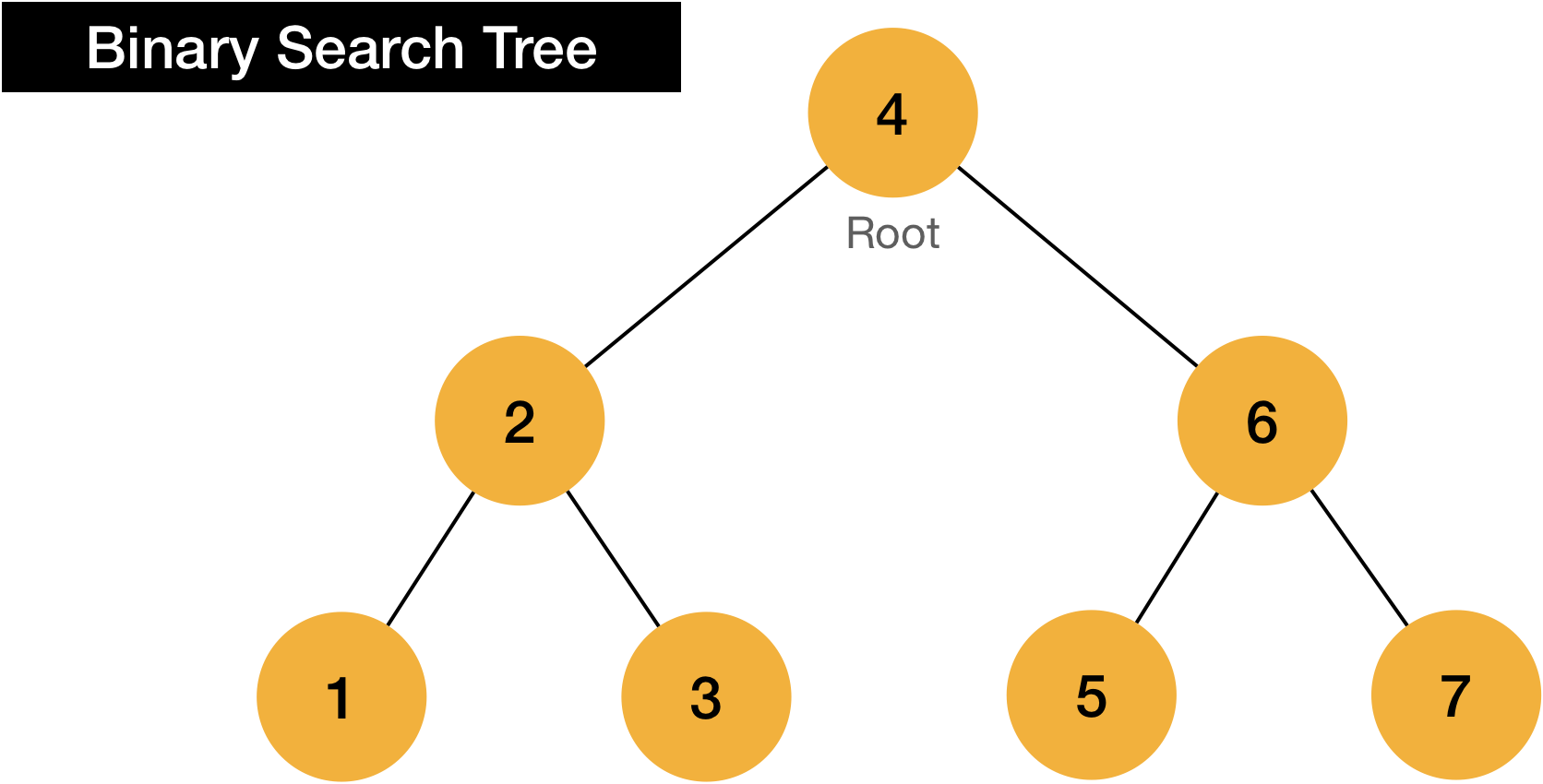
Let’s see how it works step by step.
- If tree is empty, data will be linked with root as normal binary tree was in previous section
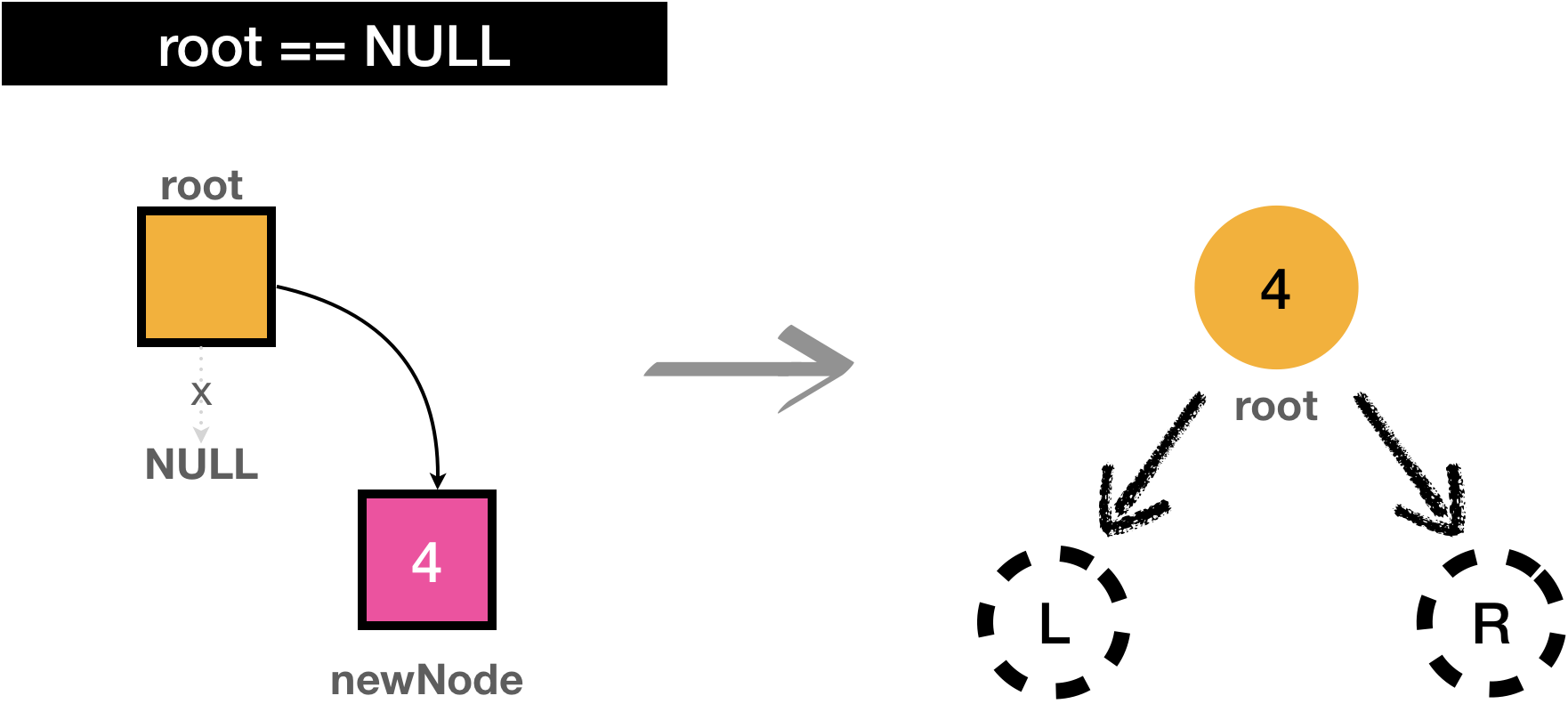
- if new data is smaller than root data, it will traverse to the left, otherwise it will traverse to the right
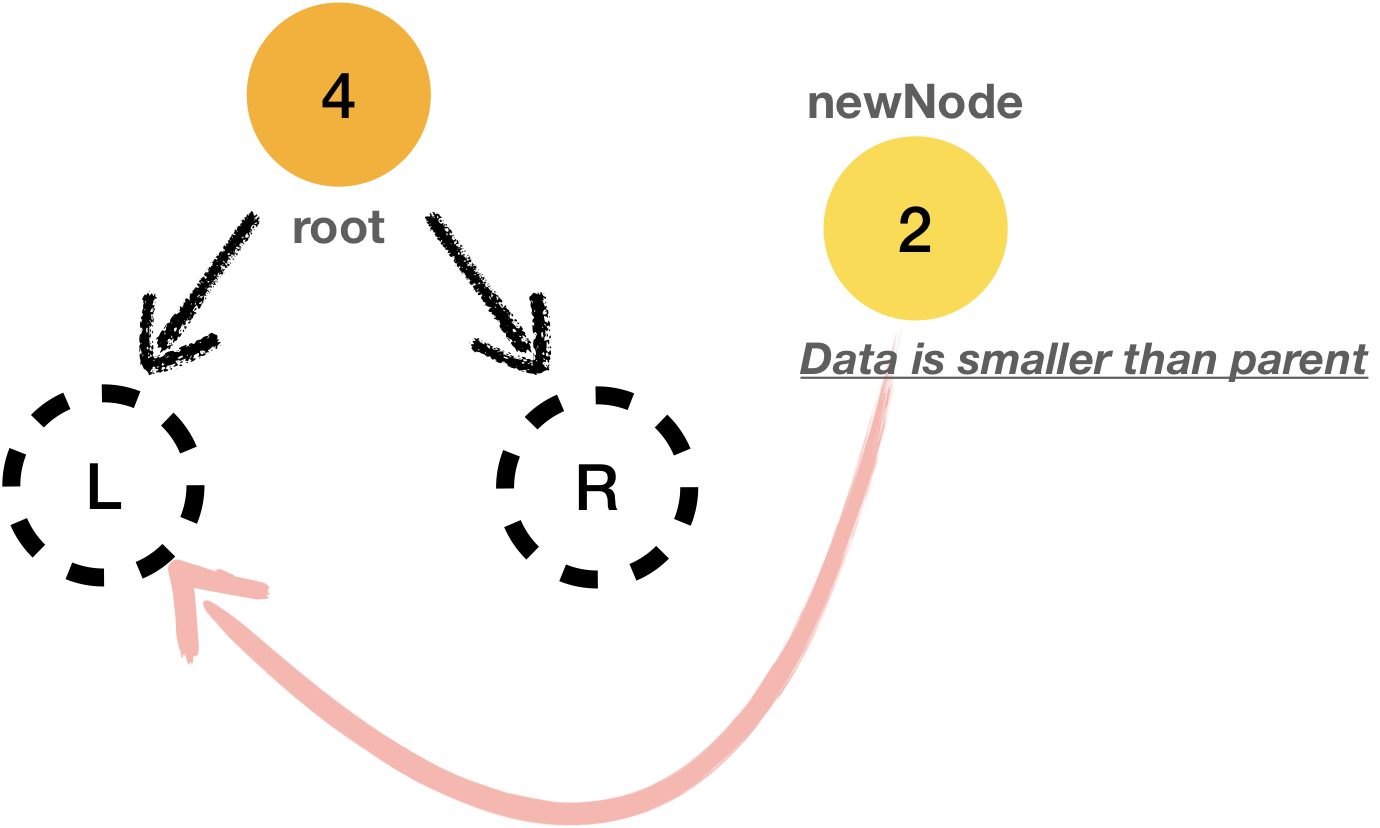
- if there is no existing data to compare, new data will be placed in where it traverse last
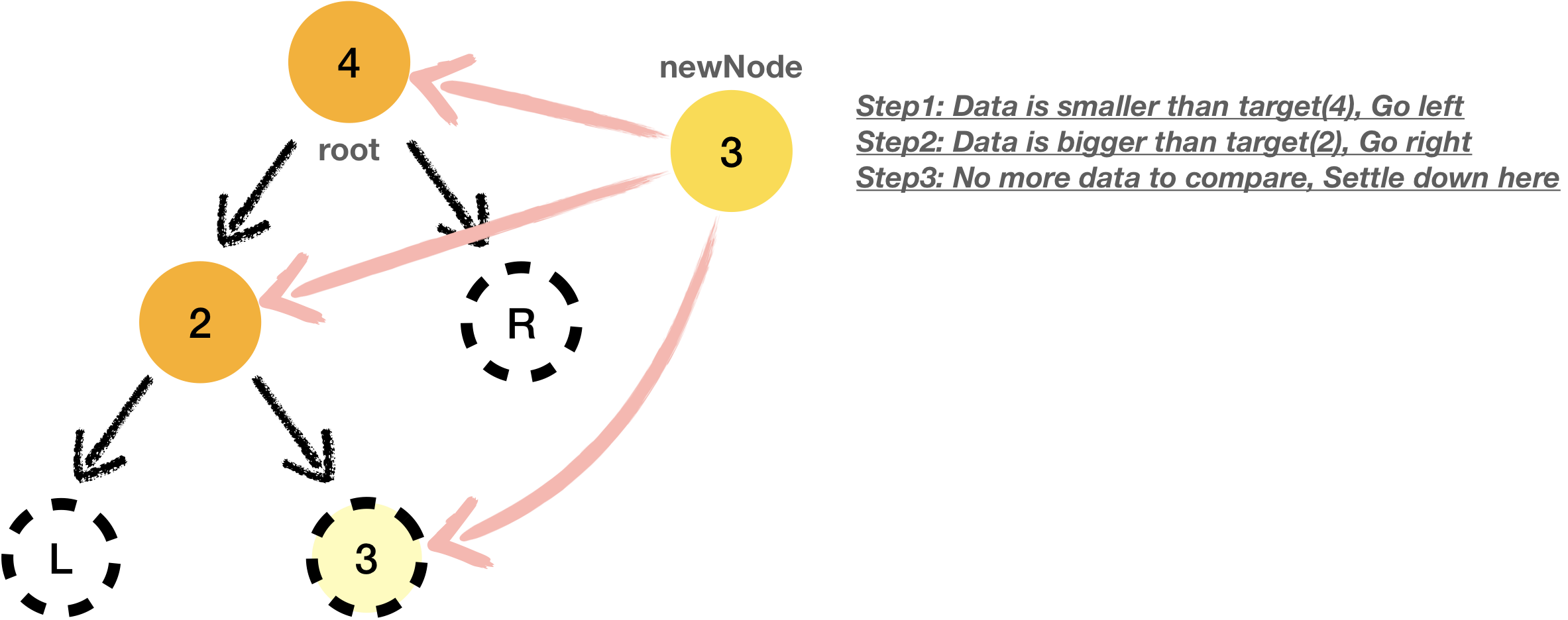
As I commented in the figure above, newNode will be settled down on where is NULL.
What kind of benefit can we achieve with this kind of complicated operation then?
In a word, we can find the data in O(Log2N). N is number of nodes, which means if you have,
- below 8 nodes, you can find any node in 3 trials
- below 1024 nodes, you can find any node in 10 trials of visiting nodes which is way faster than other search algorithm.
2.3 Implementation
Before we start implementation of this, there is constraint that every node‘s value or whatever you are going to use as key must be unique, otherwise code does not know where it should go from left or right. Please keep this in your mind while you implement the code.
There is no change on initiation part, let’s reuse the code for definition and declaration.
typedef struct _node{
int data; // user data which will be stored in the each node
struct _node *left; // pointer which is pointing left child
struct _node *right; // right child
} Node; // naming `struct _node`
Node *root = NULL; //declaration of root node with pointer
Main point for building binary search tree is making the binary search tree format while inserting the newNode.
2.3.1 Data Insertion
void insert_data(int data){
Node *newNode = new_node(data);
Node *traverse_ptr = root;
Node *parent = traverse_ptr;
if(root == NULL) {
root = newNode;
return;
}
while(traverse_ptr){
parent = traverse_ptr;
if(data < traverse_ptr->data){ // traverse to the left
traverse_ptr = traverse_ptr->left;
} else if(traverse_ptr->data < data) { // traverse to the right
traverse_ptr = traverse_ptr->right;
} else { // key value must be unique, otherwise insert operation will be stopped
return;
}
}
if(data < parent->data) parent->left = newNode;
else parent->right = newNode;
}
2.4 Improvement
I don’t like duplication. It makes me sick, It makes everybody sick actually. Above code has three significant problems, did you notice where we can improve?
- Of course, no problem at all from the functionality pespective
There are two points where I want to improve,
- First of all, It looks bad if I need to use additional pointer for storing parent node
- Second, There is duplication on logic for comparing the values between exisiting data and new data. Even though it found where the
newNodeshould be linked, it is comparing the values again after while loop - Third, I just want to make the code as common, I don’t want to put any code for specific cases. In this code,
if(root == NULL)log is the case.
Please think how you can improve this code and remove any redundant code.
2.4.1 Removal of parent pointer
I know there are several duplication in the code, but how can I remove and efficinate it?

The key is double pointer.
Double pointer is the pointer points pointer‘s box. What does it mean :-) ?
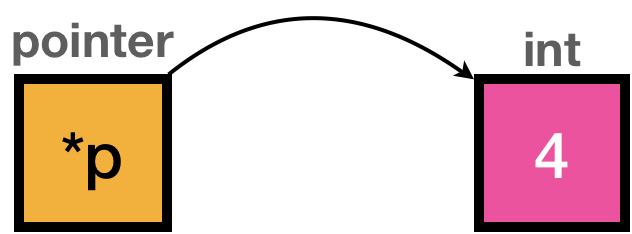
Pointer is pointing the memory of integer value in above example, and I would say yellow box is for the memory for pointer p
Pointer p itself also needs memory location, it also has memory address.
and double pointer which we are going to use to remove the redundancy will point out the yellow box like below.

Okay, you migh already know what the double pointer is, but how can we use this to make it efficient?
Open your eyes and let’s see how the magic works.
void insert_data(int data){
Node *newNode = new_node(data);
Node **traverse_ptr = &root; // 0. Make traverse_ptr as double pointer, add & so that double pointer can point address of root pointer
//Node *parent = traverse_ptr; // 1. Remove parent pointer
if(root == NULL) {
root = newNode;
return;
}
while(*traverse_ptr){ //2. Add *
//parent = traverse_ptr; //3. Remove storing the previous node in parent pointer
if(data < (*traverse_ptr)->data){ // 4. Add *
traverse_ptr = &(*traverse_ptr)->left; // 5. Add & to store address of left pointer
} else if((*traverse_ptr)->data < data) { // 6. Add *
traverse_ptr = &(*traverse_ptr)->right; // 7. Add & to store address of right pointer to the double pointer (traverse_ptr)
} else {
return;
}
}
*traverse_ptr = newNode; // 8. Assign newNode to the box where double pointer was pointing out
/***Remove the duplicated operation***/
//
//if(data < parent->data) parent->left = newNode;
//else parent->right = newNode;
//
/*************************************/
}
Step 8 might be quite complicated, but if you remind double pointer is pointing the pointer’s memory, you can easily understand how it is possible.
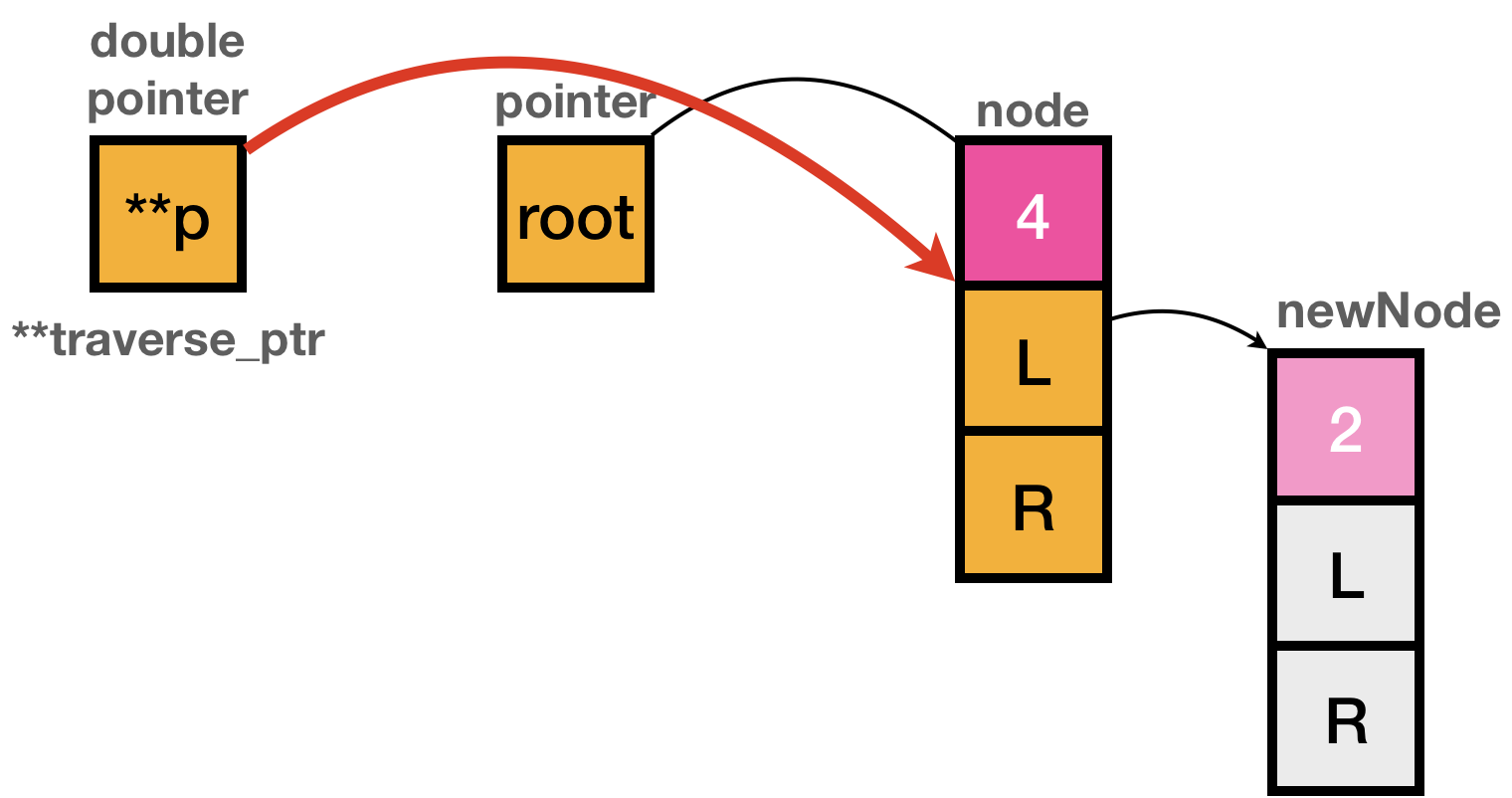
traverse_ptr was pointing out left pointer’s memory address. In this example, newNode with 2 should be linked with left pointer in node 4.
While logic was traversing the nodes, address of pointer box, L box in above example, is stored in **traverse_ptr.
To make node 4’s left is pointing newNode, we can get left pointer from the *traverse_ptr.
Let’s say L = NULL,
In previous code, code will exit the while loop if traverse_ptr is NULL.
As traverse_ptr is just set as NULL, there was no way to check what was the pointing out that NULL.
However, with double pointer, we can assign newNode on what was pointing out the NULL.
This is quite simple method, but not easy to come up with if you face this problem.
2.4.2 Removal of duplicated logic
During overcoming above problem, 2.4.1, we were able to remove duplicated logic of comparison, which was comparing the values again after while loop.
2.4.3 Making the logic for common use
Now it’s time to remove the specific code for root == NULL. As we used double pointer,
we can easily remove below part.
…
/*
if(root == NULL) {
root = newNode;
return;
}
*/
…
It was already covered as a part of using *traverse_ptr for the while loop exit condition.
Initially, root was initialized as NULL and &root was assigned to Node ** traverse_ptr.
Which means, while loop will immediately exit if there is no data in the tree.
Later, newNode address was assigned to *traverse_ptr which will be root.
…
*traverse_ptr = newNode;
…
Now we were able to improve the codes from the removal of redundant and removal of specific case point of view.
This will be the final code snippet for it.
void insert_data(int data){
Node *newNode = new_node(data);
Node **traverse_ptr = &root;
while(*traverse_ptr){ //2. Add *
if(data < (*traverse_ptr)->data){
traverse_ptr = &(*traverse_ptr)->left;
} else if((*traverse_ptr)->data < data) {
traverse_ptr = &(*traverse_ptr)->right;
} else {
return;
}
}
*traverse_ptr = newNode;
}
2.5 Worst case
Every algorithm has pros and cons, and binary search tree can not avoid this problem.
Ideally, if we want to achieve O(Log2N) performance with binary search tree, well-balanced tree shape is required like multiple examples I shared above.
Let’s assume insert data is already sorted, and it is inserted in order with our function.
int main(){
int samples[] = {1, 2, 3, 4, 5, 6, 7};
for (int i=0;i<7;i++){
insert_data(samples[i]);
}
return 0;
}
What will happen?
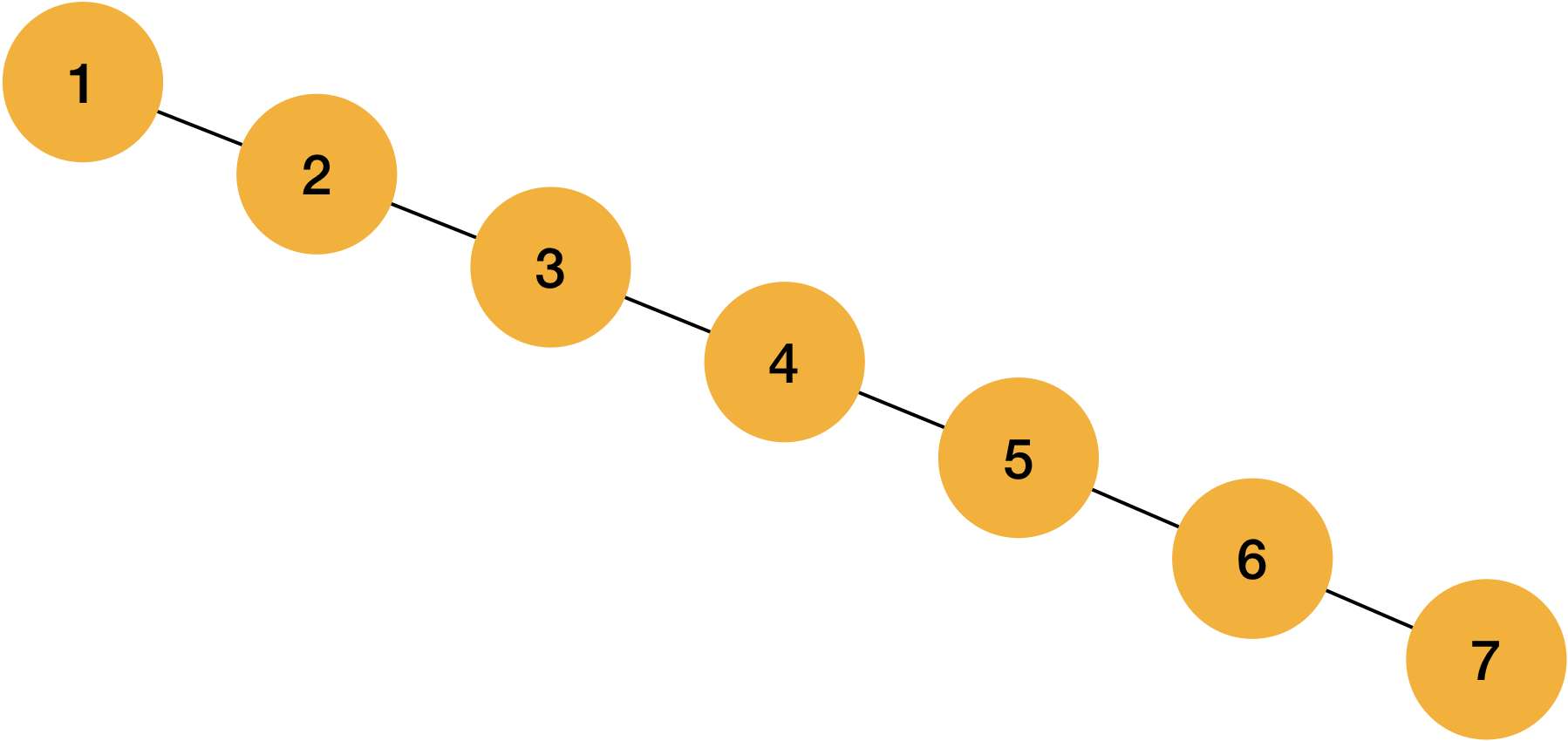
How does it look like? It was binary search tree, but no difference from linked list, and it spends more memories for not in used left pointers.
Let’s think how the search performace will be.
If I have to find number 7, it will take O(N) as it will traverse the tree from the root=1, and move to the right over and over again until it reaches to number 7.
How can we overcome this problem?
Let’s talk about Rebalancing technic for this matter.
2.5.1 Improvement - Rebalancing function
What is rebalancing?
It is literally rebalancing the data in the binary search tree to keep it as the form of the best performance for searching.
In this post, we will create coverter from the tree to array and again to tree, so that unbalanced tree form will be maintained as well-balanced form.
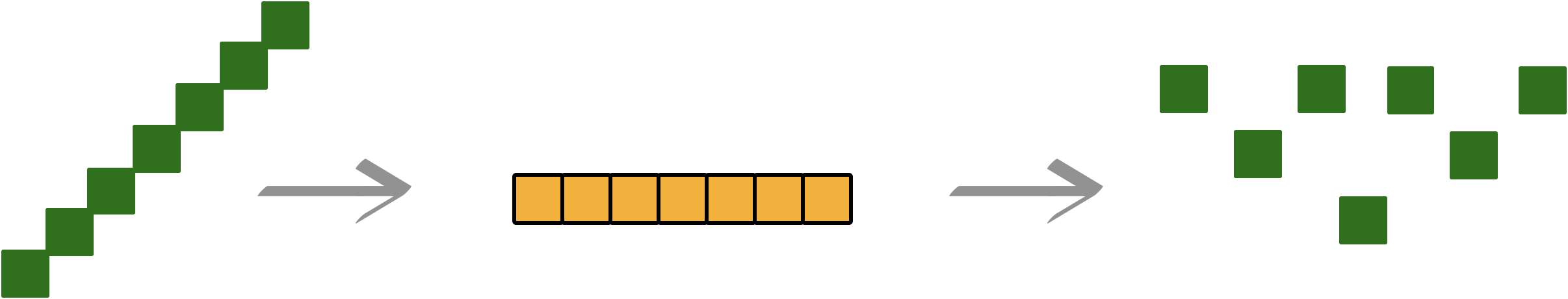
Will this be efficient?
We can not run this rebalancing function whenever there is new data, but at least we can reform the tree shape every certain period of the time, and our data structure will show best performance at least in the situation that data is balanced.
Let’s deep dive how we can implement balancing function.
2.5.1.1 Covert tree to array
Before we go, I would like you to remind the section 1.3.3.2 In order traverse.
Characteristics of Binary search tree is, even if data is unbalanced, anyway it’s always following the rule that smaller value will be on the left and bigger value will be on the right from the mid value.( Notice: Example in 1.3.3.2 In order traverse is binary tree, but not binary search tree, please keep in mind)
Which means, if you traverse the data in order, it will be already sorted.
Let’s see multiple examples.
Example #1
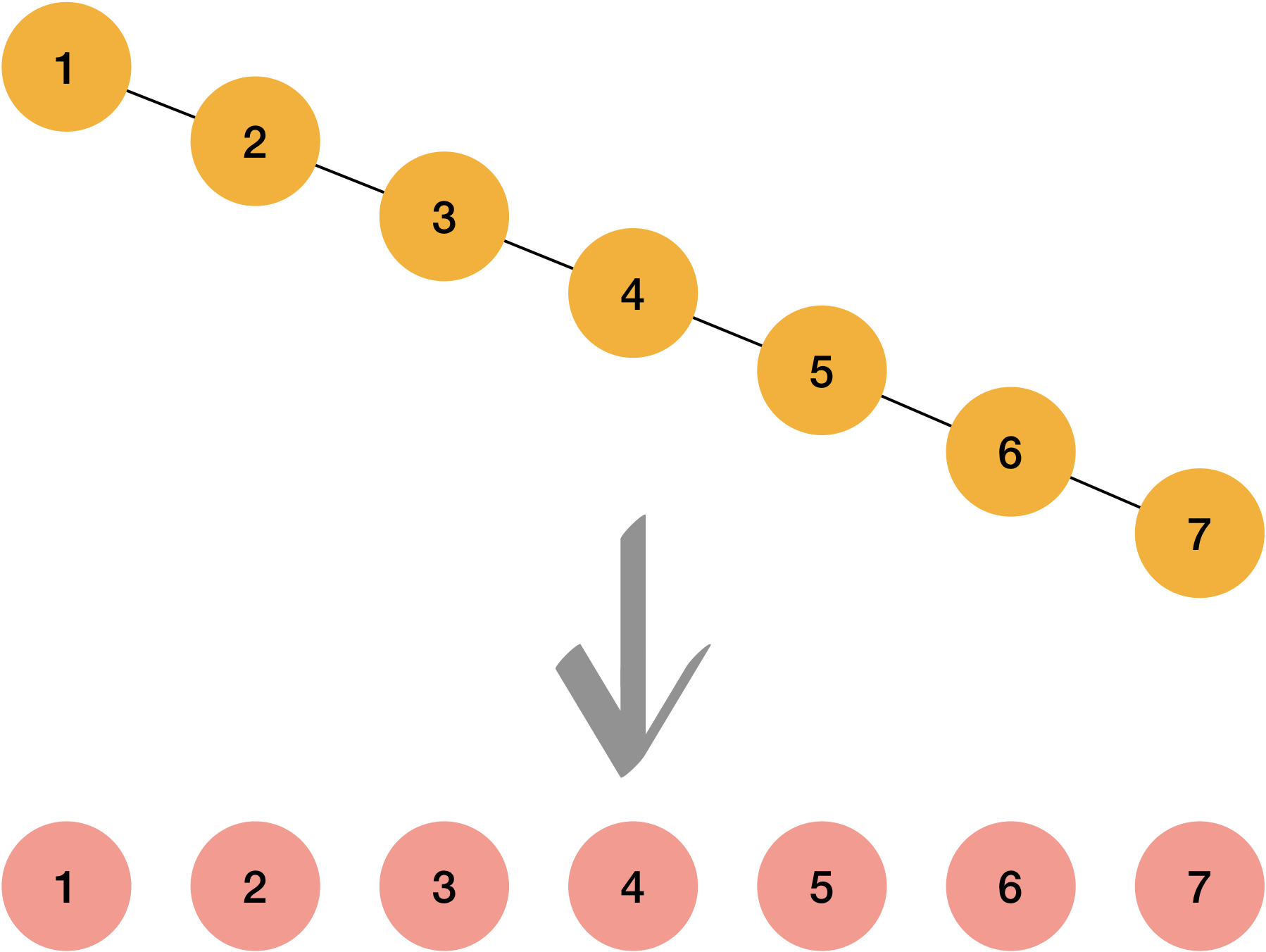
Example #2
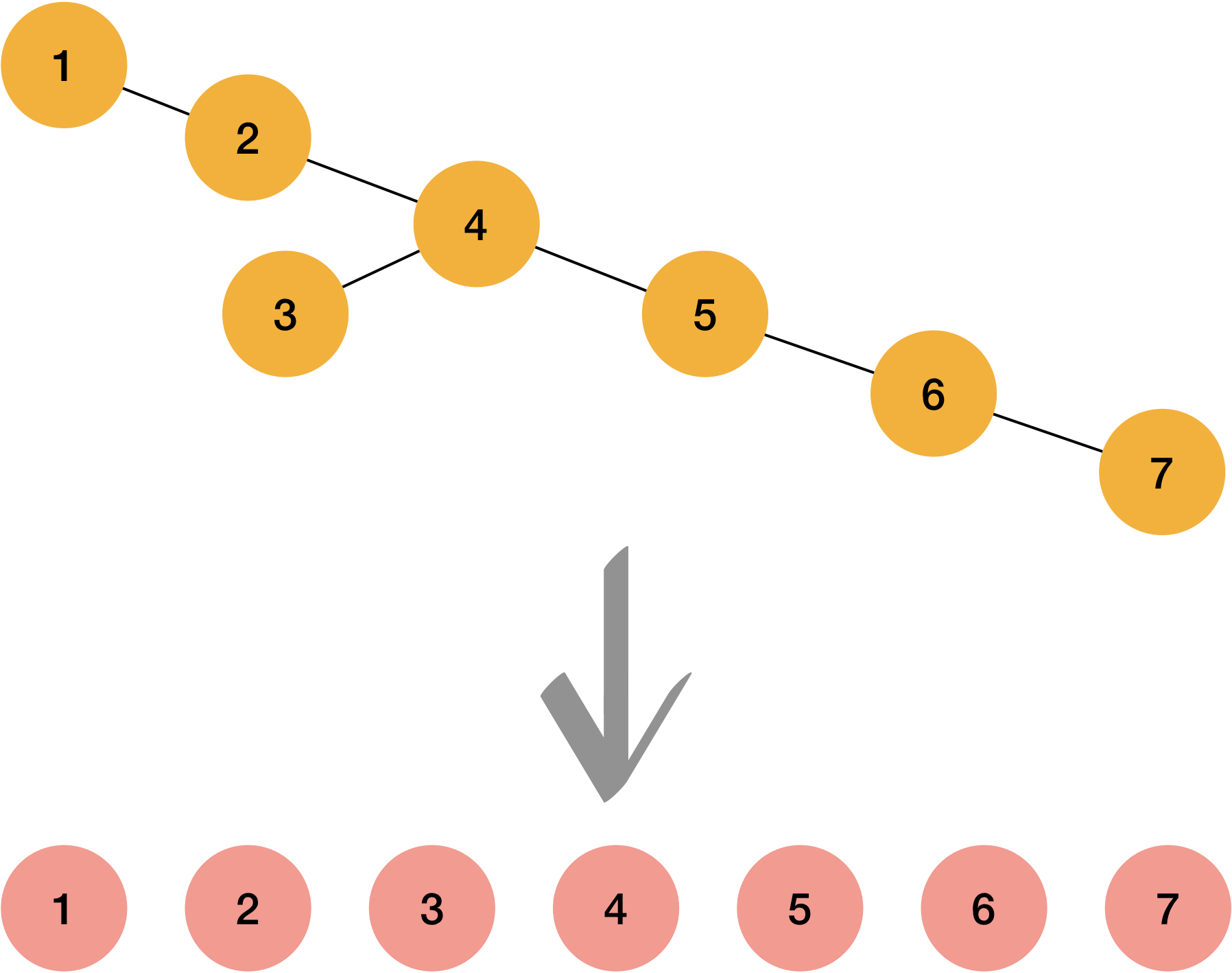
Example #3
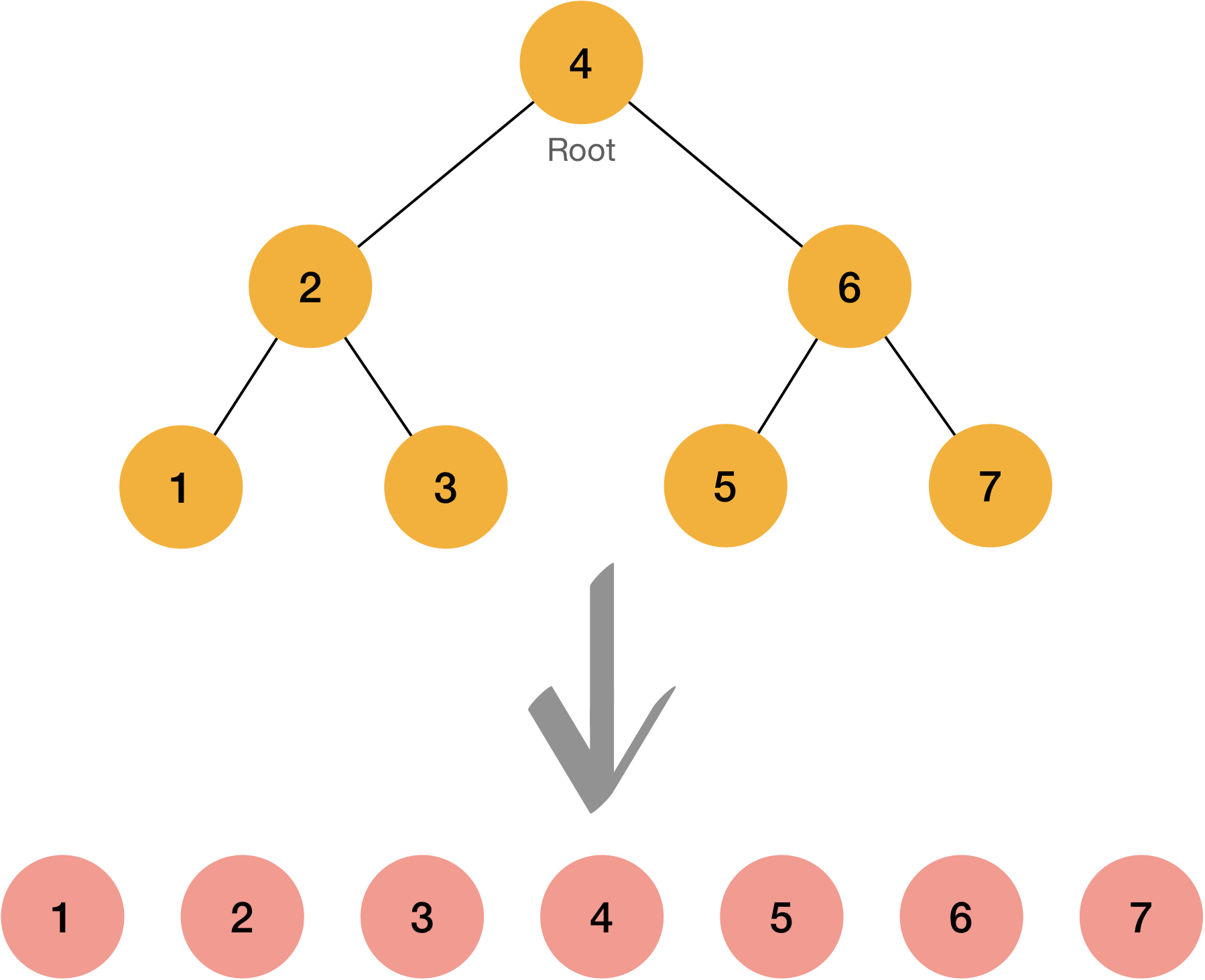
If you see the result carefully, you will realize that output is already in ordered.
We can easily covert unbalanced form of binary search tree with In order traverse.
void __convert_to_array(Node *node, int *idx,int *arr){
if(node == NULL) return;
__convert_to_array(node->left, idx, arr);
arr[(*idx)++] = node->data;
__convert_to_array(node->right, idx, arr);
}
__covert_to_array function traverses the tree with in-order and store the data in array delivered over the parameter.
idx is also needed to be delivered as traversing the tree requires recursive calls.
Let’s say coverting from unbalanced tree to array is done.
Next step will be converting from the array to the binary search tree with balanced form.
void __convert_to_bsearch_tree(int *arr, int e){
int end = e;
int mid = e / 2;
if(mid == start) return;
insert_data(arr[mid]);
__convert_to_bsearch_tree(arr, mid);
__convert_to_bsearch_tree(arr + mid + 1, e - mid - 1);
}
Now, it’s time to write the rebalance code.
void rebalance_bsTree(){
// temp array
int arr[LENGTH];
int len = 0;
// convert to the array
__convert_to_array(root, &len, arr);
//init the root
root = NULL;
// covert to the bsTree
__convert_to_bsearch_tree(arr, len);
}
3. Is this data structure + improvement perfect?
It basically discards overall tree and regenerate new one, which takes quite long time if there are millions of data. Moreover, this rebalancing is not able to work in realtime, which means this rebalancing function should be called weekly or monthly.
But if sorted data keeps being inserted to the data structure, tree will be immediately unblanced even if it is just balanced.
I would say, it still has a problem and this is not the best solution for managing the huge amount of data in the database system.
So as per this rebalancing requirement, new tree structure which came up to cope with realtime issue was introduced, it is called Red-Black Tree.
Let’s deep dive in Red-Black Tree in the next post, and compare how Red-Black Tree improves problems and see the differences.
And don’t forget to remind what the Binary Tree & Binary Search Tree are before you read next post.
See you soon,
Happy coding!
Regards,
Jeesub
Leave a comment